吴恩达机器学习课程笔记_自变量t上标-程序员宅基地
技术标签: 机器学习 SHU老黑的大学之路
吴恩达机器学习
几乎每一个和我讨论过的人都同意,人生的最糟糕时期是在11岁到14岁。——《黑客与画家》
学习资料
课程
主成分数据选择那里有一节课没有字幕,建议移步Coursera
黄海广笔记
第0天
搜集信息,注册Coursera,申请奖学金,安排学习计划。(2h)
引言(Introduction)
1.1 欢迎
参考视频: 1 - 1 - Welcome (7 min).mkv
第一个视频主要讲了什么是机器学习,机器学习能做些什么事情。
1.2 机器学习是什么?
第一个机器学习的定义来自于Arthur Samuel。他定义机器学习为,在进行特定编程的情况下,给予计算机学习能力的领域。Samuel的定义可以回溯到50年代,他编写了一个西洋棋程序。
另一个年代近一点的定义,由Tom Mitchell提出,来自卡内基梅隆大学,Tom定义的机器学习是,一个好的学习问题定义如下,他说,一个程序被认为能从经验E中学习,解决任务T,达到性能度量值P,当且仅当,有了经验E后,经过P评判,程序在处理T时的性能有所提升。我认为经验E 就是程序上万次的自我练习的经验而任务T 就是下棋。性能度量值P呢,就是它在与一些新的对手比赛时,赢得比赛的概率。
目前存在几种不同类型的学习算法。主要的两种类型被我们称之为监督学习和无监督学习。此外你将听到诸如,强化学习和推荐系统等各种术语。这些都是机器学习算法的一员,以后我们都将介绍到,但学习算法最常用两个类型就是监督学习、无监督学习。我会在接下来的两个视频中给出它们的定义。本课中,我们将花费最多的精力来讨论这两种学习算法。而另一个会花费大量时间的任务是了解应用学习算法的实用建议。
1.3 监督学习
监督学习指的就是我们给学习算法一个数据集。这个数据集由“正确答案”组成。
回归这个词的意思是,我们在试着推测出这一系列连续值属性。
分类指的是,我们试着推测出离散的输出值:0或1良性或恶性,而事实上在分类问题中,输出可能不止两个值。
1.4 无监督学习
所以这个就是无监督学习,因为我们没有提前告知算法一些信息,比如,这是第一类的人,那些是第二类的人,还有第三类,等等。我们只是说,是的,这是有一堆数据。我不知道数据里面有什么。我不知道谁是什么类型。我甚至不知道人们有哪些不同的类型,这些类型又是什么。但你能自动地找到数据中的结构吗?就是说你要自动地聚类那些个体到各个类,我没法提前知道哪些是哪些。因为我们没有给算法正确答案来回应数据集中的数据,所以这就是无监督学习。
鸡尾酒宴问题
第1天
单变量线性回归(Linear Regression with One Variable)
2.1 模型表示
2.2 代价函数
接下来我们会引入一些术语我们现在要做的便是为我们的模型选择合适的参数(parameters)
我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度,模型所预测的值与训练集中实际值之间的差距(下图中蓝线所指)就是建模误差(modeling error)。
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。
代价函数也被称作平方误差函数,有时也被称为平方误差代价函数。我们之所以要求出误差的平方和,是因为误差平方代价函数,对于大多数问题,特别是回归问题,都是一个合理的选择。还有其他的代价函数也能很好地发挥作用,但是平方误差代价函数可能是解决回归问题最常用的手段了。
2.3 代价函数的直观理解I
2.4 代价函数的直观理解II
2.5 梯度下降
梯度下降是一个用来求函数最小值的算法
梯度下降背后的思想是:开始时我们随机选择一个参数的组合计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到找到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值。
批量梯度下降(batch gradient descent)算法的公式为:
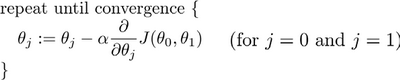
其中是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。


在梯度下降算法中,这是正确实现同时更新的方法。我不打算解释为什么你需要同时更新,同时更新是梯度下降中的一种常用方法。我们之后会讲到,同步更新是更自然的实现方法。当人们谈到梯度下降时,他们的意思就是同步更新。
2.6 梯度下降的直观理解
学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。
如果太小了,即我的学习速率太小,结果就是只能这样像小宝宝一样一点点地挪动,去努力接近最低点,这样就需要很多步才能到达最低点,所以如果太小的话,可能会很慢,因为它会一点点挪动,它会需要很多步才能到达全局最低点。
如果太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛,下一次迭代又移动了一大步,越过一次,又越过一次,一次次越过最低点,直到你发现实际上离最低点越来越远,所以,如果太大,它会导致无法收敛,甚至发散。
2.7 梯度下降(gradient descent)的线性回归
实际上,在机器学习中,通常不太会给算法起名字,但这个名字”批量梯度下降”,指的是在梯度下降的每一步中,我们都用到了所有的训练样本,在梯度下降中,在计算微分求导项时,我们需要进行求和运算,所以,在每一个单独的梯度下降中,我们最终都要计算这样一个东西,这个项需要对所有m个训练样本求和。
线性代数回顾(Linear Algebra Review)
matlab中矩阵转置:直接打一撇,x=y'。
多变量线性回归(Linear Regression with Multiple Variables)
4.1 多维特征
4.2 多变量梯度下降
与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价函数是所有建模误差的平方和
我们的目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数。
Python 代码:
def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))
4.3 梯度下降法实践1-特征缩放
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
4.4 梯度下降法实践2-学习率
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,我们不能提前预知,我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。
梯度下降算法的每次迭代受到学习率的影响,如果学习率a过小,则达到收敛所需的迭代次数会非常高;如果学习率a过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
4.5 特征和多项式回归
注:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。
4.6 正规方程Normal Equation
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的: ∂ ∂ θ j J ( θ j ) = 0 \frac{\partial}{\partial{\theta_{j}}}J\left( {\theta_{j}} \right)=0 ∂θj∂J(θj)=0
利用正规方程解出向量 θ = ( X T X ) − 1 X T y \theta ={ {\left( {X^T}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy 。 上标T代表矩阵转置,上标-1 代表矩阵的逆。
总结一下,只要特征变量的数目并不大,标准方程是一个很好的计算参数的替代方法。具体地说,只要特征变量数量小于一万,我通常使用标准方程法,而不使用梯度下降法。
4.7 正规方程及不可逆性(可选)
增加内容:
θ = ( X T X ) − 1 X T y \theta ={ {\left( {X^{T}}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy 的推导过程:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{ { {\left( {h_{\theta}}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2 其中: h θ ( x ) = θ T X = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n {h_{\theta}}\left( x \right)={\theta^{T}}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θTX=θ0x0+θ1x1+θ2x2+...+θnxn
将向量表达形式转为矩阵表达形式,则有 J ( θ ) = 1 2 ( X θ − y ) 2 J(\theta )=\frac{1}{2}{ {\left( X\theta -y\right)}^{2}} J(θ)=21(Xθ−y)2 ,其中 X X X为 m m m行 n n n列的矩阵( m m m为样本个数, n n n为特征个数), θ \theta θ为 n n n行1列的矩阵, y y y为 m m m行1列的矩阵,对 J ( θ ) J(\theta ) J(θ)进行如下变换
J ( θ ) = 1 2 ( X θ − y ) T ( X θ − y ) J(\theta )=\frac{1}{2}{ {\left( X\theta -y\right)}^{T}}\left( X\theta -y \right) J(θ)=21(Xθ−y)T(Xθ−y)
= 1 2 ( θ T X T − y T ) ( X θ − y ) =\frac{1}{2}\left( { {\theta }^{T}}{ {X}^{T}}-{ {y}^{T}} \right)\left(X\theta -y \right) =21(θTXT−yT)(Xθ−y)
= 1 2 ( θ T X T X θ − θ T X T y − y T X θ − y T y ) =\frac{1}{2}\left( { {\theta }^{T}}{ {X}^{T}}X\theta -{ {\theta}^{T}}{ {X}^{T}}y-{ {y}^{T}}X\theta -{ {y}^{T}}y \right) =21(θTXTXθ−θTXTy−yTXθ−yTy)
接下来对 J ( θ ) J(\theta ) J(θ)偏导,需要用到以下几个矩阵的求导法则:
d A B d B = A T \frac{dAB}{dB}={ {A}^{T}} dBdAB=AT
d X T A X d X = 2 A X \frac{d{ {X}^{T}}AX}{dX}=2AX dXdXTAX=2AX
所以有:
∂ J ( θ ) ∂ θ = 1 2 ( 2 X T X θ − X T y − ( y T X ) T − 0 ) \frac{\partial J\left( \theta \right)}{\partial \theta }=\frac{1}{2}\left(2{ {X}^{T}}X\theta -{ {X}^{T}}y -{}({ {y}^{T}}X )^{T}-0 \right) ∂θ∂J(θ)=21(2XTXθ−XTy−(yTX)T−0)
= 1 2 ( 2 X T X θ − X T y − X T y − 0 ) =\frac{1}{2}\left(2{ {X}^{T}}X\theta -{ {X}^{T}}y -{ {X}^{T}}y -0 \right) =21(2XTXθ−XTy−XTy−0)
= X T X θ − X T y ={ {X}^{T}}X\theta -{ {X}^{T}}y =XTXθ−XTy
令 ∂ J ( θ ) ∂ θ = 0 \frac{\partial J\left( \theta \right)}{\partial \theta }=0 ∂θ∂J(θ)=0,
则有 θ = ( X T X ) − 1 X T y \theta ={ {\left( {X^{T}}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy
Octave教程(Octave Tutorial)
现在大家都用python了,octave不想再浪费时间去搞了,反正作业可以用matlab一样可以做。5.6向量化看一下,当你使用向量化地实现线性回归,通常运行速度就会比你以前用你的for循环快的多,也就是自己写代码更新。
第2天
逻辑回归(Logistic Regression)
6.1 分类问题
我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法,这是目前最流行使用最广泛的一种学习算法。
我们从二元的分类问题开始讨论。
我们将因变量(dependent variable)可能属于的两个类分别称为负向类(negative class)和正向类(positive class),则因变量,其中 0 表示负向类,1 表示正向类。
顺便说一下,逻辑回归算法是分类算法,我们将它作为分类算法使用。有时候可能因为这个算法的名字中出现了“回归”使你感到困惑,但逻辑回归算法实际上是一种分类算法
6.2 假说表示
逻辑回归模型的假设是: h θ ( x ) = g ( θ T X ) h_\theta \left( x \right)=g\left(\theta^{T}X \right) hθ(x)=g(θTX) 其中: X X X 代表特征向量 g g g 代表逻辑函数(logistic function)是一个常用的逻辑函数为S形函数(Sigmoid function),公式为: g ( z ) = 1 1 + e − z g\left( z \right)=\frac{1}{1+{ {e}^{-z}}} g(z)=1+e−z1。
h θ ( x ) h_\theta \left( x \right) hθ(x)的作用是,对于给定的输入变量,根据选择的参数计算输出变量=1的可能性(estimated probablity)即 h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_\theta \left( x \right)=P\left( y=1|x;\theta \right) hθ(x)=P(y=1∣x;θ) 例如,如果对于给定的 x x x,通过已经确定的参数计算得出 h θ ( x ) = 0.7 h_\theta \left( x \right)=0.7 hθ(x)=0.7,则表示有70%的几率 y y y为正向类,相应地 y y y为负向类的几率为1-0.7=0.3。
6.3 判定边界
现在讲下决策边界(decision boundary)的概念。这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。
因为需要用曲线才能分隔 y = 0 y=0 y=0 的区域和 y = 1 y=1 y=1 的区域,我们需要二次方特征: h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 2 2 ) {h_\theta}\left( x \right)=g\left( {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}}+{\theta_{3}}x_{1}^{2}+{\theta_{4}}x_{2}^{2} \right) hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x22)是[-1 0 0 1 1],则我们得到的判定边界恰好是圆点在原点且半径为1的圆形。
我们可以用非常复杂的模型来适应非常复杂形状的判定边界。
6.4 代价函数
定义用来拟合参数的优化目标或者叫代价函数,这便是监督学习问题中的逻辑回归模型的拟合问题。
对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。理论上来说,我们也可以对逻辑回归模型沿用这个定义,但是问题在于,当我们将 h θ ( x ) = 1 1 + e − θ T x {h_\theta}\left( x \right)=\frac{1}{1+{e^{-\theta^{T}x}}} hθ(x)=1+e−θTx1带入到这样定义了的代价函数中时,我们得到的代价函数将是一个非凸函数(non-convexfunction)。
这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。
线性回归的代价函数为: J ( θ ) = 1 m ∑ i = 1 m 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{\frac{1}{2}{ {\left( {h_\theta}\left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}} J(θ)=m1i=1∑m21(hθ(x(i))−y(i))2 。 我们重新定义逻辑回归的代价函数为: J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) ) , y ( i ) ) J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{ {Cost}\left( {h_\theta}\left( {x}^{\left( i \right)} \right),{y}^{\left( i \right)} \right)} J(θ)=m1i=1∑mCost(hθ(x(i)),y(i)),其中
这样构建的 C o s t ( h θ ( x ) , y ) Cost\left( {h_\theta}\left( x \right),y \right) Cost(hθ(x),y)函数的特点是:当实际的 y = 1 y=1 y=1 且 h θ ( x ) {h_\theta}\left( x \right) hθ(x)也为 1 时误差为 0,当 y = 1 y=1 y=1 但 h θ ( x ) {h_\theta}\left( x \right) hθ(x)不为1时误差随着 h θ ( x ) {h_\theta}\left( x \right) hθ(x)变小而变大;当实际的 y = 0 y=0 y=0 且 h θ ( x ) {h_\theta}\left( x \right) hθ(x)也为 0 时代价为 0,当 y = 0 y=0 y=0 但 h θ ( x ) {h_\theta}\left( x \right) hθ(x)不为 0时误差随着 h θ ( x ) {h_\theta}\left( x \right) hθ(x)的变大而变大。 将构建的 C o s t ( h θ ( x ) , y ) Cost\left( {h_\theta}\left( x \right),y \right) Cost(hθ(x),y)简化如下: C o s t ( h θ ( x ) , y ) = − y × l o g ( h θ ( x ) ) − ( 1 − y ) × l o g ( 1 − h θ ( x ) ) Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right) Cost(hθ(x),y)=−y×log(hθ(x))−(1−y)×log(1−hθ(x)) 带入代价函数得到: J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{ {y}^{(i)}}\log \left( {h_\theta}\left( { {x}^{(i)}} \right) \right)-\left( 1-{ {y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( { {x}^{(i)}} \right) \right)]} J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))] 即: J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{ {y}^{(i)}}\log \left( {h_\theta}\left( { {x}^{(i)}} \right) \right)+\left( 1-{ {y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( { {x}^{(i)}} \right) \right)]} J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
在得到这样一个代价函数以后,我们便可以用梯度下降算法来求得能使代价函数最小的参数了。算法为:
Repeat { θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j} J(\theta) θj:=θj−α∂θj∂J(θ) (simultaneously update all ) }
求导后得到:
Repeat { θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j := \theta_j - \alpha \frac{1}{m}\sum\limits_{i=1}^{m}{ {\left( {h_\theta}\left( \mathop{x}^{\left( i \right)} \right)-\mathop{y}^{\left( i \right)} \right)}}\mathop{x}_{j}^{(i)} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i) (simultaneously update all ) }
在这个视频中,我们定义了单训练样本的代价函数,凸性分析的内容是超出这门课的范围的,但是可以证明我们所选的代价值函数会给我们一个凸优化问题。代价函数 J ( θ ) J(\theta) J(θ)会是一个凸函数,并且没有局部最优值。
推导过程:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{ {y}^{(i)}}\log \left( {h_\theta}\left( { {x}^{(i)}} \right) \right)+\left( 1-{ {y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( { {x}^{(i)}} \right) \right)]} J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))] 考虑: h θ ( x ( i ) ) = 1 1 + e − θ T x ( i ) {h_\theta}\left( { {x}^{(i)}} \right)=\frac{1}{1+{ {e}^{-{\theta^T}{ {x}^{(i)}}}}} hθ(x(i))=1+e−θTx(i)1 则: y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) { {y}^{(i)}}\log \left( {h_\theta}\left( { {x}^{(i)}} \right) \right)+\left( 1-{ {y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( { {x}^{(i)}} \right) \right) y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i))) = y ( i ) log ( 1 1 + e − θ T x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − 1 1 + e − θ T x ( i ) ) ={ {y}^{(i)}}\log \left( \frac{1}{1+{ {e}^{-{\theta^T}{ {x}^{(i)}}}}} \right)+\left( 1-{ {y}^{(i)}} \right)\log \left( 1-\frac{1}{1+{ {e}^{-{\theta^T}{ {x}^{(i)}}}}} \right) =y(i)log(1+e−θTx(i)1)+(1−y(i))log(1−1+e−θTx(i)1) = − y ( i ) log ( 1 + e − θ T x ( i ) ) − ( 1 − y ( i ) ) log ( 1 + e θ T x ( i ) ) =-{ {y}^{(i)}}\log \left( 1+{ {e}^{-{\theta^T}{ {x}^{(i)}}}} \right)-\left( 1-{ {y}^{(i)}} \right)\log \left( 1+{ {e}^{ {\theta^T}{ {x}^{(i)}}}} \right) =−y(i)log(1+e−θTx(i))−(1−y(i))log(1+eθTx(i))
所以: ∂ ∂ θ j J ( θ ) = ∂ ∂ θ j [ − 1 m ∑ i = 1 m [ − y ( i ) log ( 1 + e − θ T x ( i ) ) − ( 1 − y ( i ) ) log ( 1 + e θ T x ( i ) ) ] ] \frac{\partial }{\partial {\theta_{j}}}J\left( \theta \right)=\frac{\partial }{\partial {\theta_{j}}}[-\frac{1}{m}\sum\limits_{i=1}^{m}{[-{ {y}^{(i)}}\log \left( 1+{ {e}^{-{\theta^{T}}{ {x}^{(i)}}}} \right)-\left( 1-{ {y}^{(i)}} \right)\log \left( 1+{ {e}^{ {\theta^{T}}{ {x}^{(i)}}}} \right)]}] ∂θj∂J(θ)=∂θj∂[−m1i=1∑m[−y(i)log(1+e−θTx(i))−(1−y(i))log(1+eθTx(i))]] = − 1 m ∑ i = 1 m [ − y ( i ) − x j ( i ) e − θ T x ( i ) 1 + e − θ T x ( i ) − ( 1 − y ( i ) ) x j ( i ) e θ T x ( i ) 1 + e θ T x ( i ) ] =-\frac{1}{m}\sum\limits_{i=1}^{m}{[-{ {y}^{(i)}}\frac{-x_{j}^{(i)}{ {e}^{-{\theta^{T}}{ {x}^{(i)}}}}}{1+{ {e}^{-{\theta^{T}}{ {x}^{(i)}}}}}-\left( 1-{ {y}^{(i)}} \right)\frac{x_j^{(i)}{ {e}^{ {\theta^T}{ {x}^{(i)}}}}}{1+{ {e}^{ {\theta^T}{ {x}^{(i)}}}}}}] =−m1i=1∑m[−y(i)1+e−θTx(i)−xj(i)e−θTx(i)−(1−y(i))1+eθTx(i)xj(i)eθTx(i)] = − 1 m ∑ i = 1 m y ( i ) x j ( i ) 1 + e θ T x ( i ) − ( 1 − y ( i ) ) x j ( i ) e θ T x ( i ) 1 + e θ T x ( i ) ] =-\frac{1}{m}\sum\limits_{i=1}^{m}{ {y}^{(i)}}\frac{x_j^{(i)}}{1+{ {e}^{ {\theta^T}{ {x}^{(i)}}}}}-\left( 1-{ {y}^{(i)}} \right)\frac{x_j^{(i)}{ {e}^{ {\theta^T}{ {x}^{(i)}}}}}{1+{ {e}^{ {\theta^T}{ {x}^{(i)}}}}}] =−m1i=1∑my(i)1+eθTx(i)xj(i)−(1−y(i))1+eθTx(i)xj(i)eθTx(i)] = − 1 m ∑ i = 1 m y ( i ) x j ( i ) − x j ( i ) e θ T x ( i ) + y ( i ) x j ( i ) e θ T x ( i ) 1 + e θ T x ( i ) =-\frac{1}{m}\sum\limits_{i=1}^{m}{\frac{ { {y}^{(i)}}x_j^{(i)}-x_j^{(i)}{ {e}^{ {\theta^T}{ {x}^{(i)}}}}+{ {y}^{(i)}}x_j^{(i)}{ {e}^{ {\theta^T}{ {x}^{(i)}}}}}{1+{ {e}^{ {\theta^T}{ {x}^{(i)}}}}}} =−m1i=1∑m1+eθTx(i)y(i)xj(i)−xj(i)eθTx(i)+y(i)xj(i)eθTx(i) = − 1 m ∑ i = 1 m y ( i ) ( 1 + e θ T x ( i ) ) − e θ T x ( i ) 1 + e θ T x ( i ) x j ( i ) =-\frac{1}{m}\sum\limits_{i=1}^{m}{\frac{ { {y}^{(i)}}\left( 1\text{+}{ {e}^{ {\theta^T}{ {x}^{(i)}}}} \right)-{ {e}^{ {\theta^T}{ {x}^{(i)}}}}}{1+{ {e}^{ {\theta^T}{ {x}^{(i)}}}}}x_j^{(i)}} =−m1i=1∑m1+eθTx(i)y(i)(1+eθTx(i))−eθTx(i)xj(i) = − 1 m ∑ i = 1 m ( y ( i ) − e θ T x ( i ) 1 + e θ T x ( i ) ) x j ( i ) =-\frac{1}{m}\sum\limits_{i=1}^{m}{({ {y}^{(i)}}-\frac{ { {e}^{ {\theta^T}{ {x}^{(i)}}}}}{1+{ {e}^{ {\theta^T}{ {x}^{(i)}}}}})x_j^{(i)}} =−m1i=1∑m(y(i)−1+eθTx(i)eθTx(i))xj(i) = − 1 m ∑ i = 1 m ( y ( i ) − 1 1 + e − θ T x ( i ) ) x j ( i ) =-\frac{1}{m}\sum\limits_{i=1}^{m}{({ {y}^{(i)}}-\frac{1}{1+{ {e}^{-{\theta^T}{ {x}^{(i)}}}}})x_j^{(i)}} =−m1i=1∑m(y(i)−1+e−θTx(i)1)xj(i) = − 1 m ∑ i = 1 m [ y ( i ) − h θ ( x ( i ) ) ] x j ( i ) =-\frac{1}{m}\sum\limits_{i=1}^{m}{[{ {y}^{(i)}}-{h_\theta}\left( { {x}^{(i)}} \right)]x_j^{(i)}} =−m1i=1∑m[y(i)−hθ(x(i))]xj(i) = 1 m ∑ i = 1 m [ h θ ( x ( i ) ) − y ( i ) ] x j ( i ) =\frac{1}{m}\sum\limits_{i=1}^{m}{[{h_\theta}\left( { {x}^{(i)}} \right)-{ {y}^{(i)}}]x_j^{(i)}} =m1i=1∑m[hθ(x(i))−y(i)]xj(i)
注:虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样,但是这里的 h θ ( x ) = g ( θ T X ) {h_\theta}\left( x \right)=g\left( {\theta^T}X \right) hθ(x)=g(θTX)与线性回归中不同,所以实际上是不一样的。另外,在运行梯度下降算法之前,进行特征缩放依旧是非常必要的。
一些梯度下降算法之外的选择: 除了梯度下降算法以外,还有一些常被用来令代价函数最小的算法,这些算法更加复杂和优越,而且通常不需要人工选择学习率,通常比梯度下降算法要更加快速。这些算法有:共轭梯度(Conjugate Gradient),局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS) ,fminunc是 matlab和octave 中都带的一个最小值优化函数,使用时我们需要提供代价函数和每个参数的求导,下面是 octave 中使用 fminunc 函数的代码示例
6.5 简化的成本函数和梯度下降
找出一种稍微简单一点的方法来写代价函数,来替换我们现在用的方法。同时我们还要弄清楚如何运用梯度下降法,来拟合出逻辑回归的参数。。因此,听了这节课,你就应该知道如何实现一个完整的逻辑回归算法。
C o s t ( h θ ( x ) , y ) = − y × l o g ( h θ ( x ) ) − ( 1 − y ) × l o g ( 1 − h θ ( x ) ) Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right) Cost(hθ(x),y)=−y×log(hθ(x))−(1−y)×log(1−hθ(x)) 即,逻辑回归的代价函数: C o s t ( h θ ( x ) , y ) = − y × l o g ( h θ ( x ) ) − ( 1 − y ) × l o g ( 1 − h θ ( x ) ) Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right) Cost(hθ(x),y)=−y×log(hθ(x))−(1−y)×log(1−hθ(x)) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] =-\frac{1}{m}\sum\limits_{i=1}^{m}{[{ {y}^{(i)}}\log \left( {h_\theta}\left( { {x}^{(i)}} \right) \right)+\left( 1-{ {y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( { {x}^{(i)}} \right) \right)]} =−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))] 根据这个代价函数,为了拟合出参数,该怎么做呢?我们要试图找尽量让 J ( θ ) J\left( \theta \right) J(θ) 取得最小值的参数$\theta $。 min θ J ( θ ) \underset{\theta}{\min }J\left( \theta \right) θminJ(θ) 所以我们想要尽量减小这一项,这将我们将得到某个参数$\theta $。 如果我们给出一个新的样本,假如某个特征 x x x,我们可以用拟合训练样本的参数$\theta , 来 输 出 对 假 设 的 预 测 。 另 外 , 我 们 假 设 的 输 出 , 实 际 上 就 是 这 个 概 率 值 : ,来输出对假设的预测。 另外,我们假设的输出,实际上就是这个概率值: ,来输出对假设的预测。另外,我们假设的输出,实际上就是这个概率值:p(y=1|x;\theta)$,就是关于 x x x以$\theta 为 参 数 , 为参数, 为参数,y=1$ 的概率,你可以认为我们的假设就是估计 y = 1 y=1 y=1 的概率,所以,接下来就是弄清楚如何最大限度地最小化代价函数 J ( θ ) J\left( \theta \right) J(θ),作为一个关于$\theta 的 函 数 , 这 样 我 们 才 能 为 训 练 集 拟 合 出 参 数 的函数,这样我们才能为训练集拟合出参数 的函数,这样我们才能为训练集拟合出参数\theta $。
最小化代价函数的方法,是使用梯度下降法(gradient descent)。这是我们的代价函数: J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{ {y}^{(i)}}\log \left( {h_\theta}\left( { {x}^{(i)}} \right) \right)+\left( 1-{ {y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( { {x}^{(i)}} \right) \right)]} J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
如果我们要最小化这个关于 θ \theta θ的函数值,这就是我们通常用的梯度下降法的模板。
如果你计算一下的话,你会得到这个等式: θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) {\theta_j}:={\theta_j}-\alpha \frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({ {x}^{(i)}})-{ {y}^{(i)}}){x_{j}}^{(i)}} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i) 我把它写在这里,将后面这个式子,在 i = 1 i=1 i=1 到 m m m 上求和,其实就是预测误差乘以 x j ( i ) x_j^{(i)} xj(i) ,所以你把这个偏导数项 ∂ ∂ θ j J ( θ ) \frac{\partial }{\partial {\theta_j}}J\left( \theta \right) ∂θj∂J(θ)放回到原来式子这里,我们就可以将梯度下降算法写作如下形式: θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) {\theta_j}:={\theta_j}-\alpha \frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({ {x}^{(i)}})-{ {y}^{(i)}}){x_{j}}^{(i)}} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
所以,如果你有 n n n 个特征,也就是说:参数向量$\theta 包 括 包括 包括{\theta_{0}}$ θ 1 {\theta_{1}} θ1 θ 2 {\theta_{2}} θ2 一直到 θ n {\theta_{n}} θn,那么你就需要用这个式子:
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) {\theta_j}:={\theta_j}-\alpha \frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({ {x}^{(i)}})-{ {y}^{(i)}}){ {x}_{j}}^{(i)}} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)来同时更新所有$\theta $的值。
现在,如果你把这个更新规则和我们之前用在线性回归上的进行比较的话,你会惊讶地发现,这个式子正是我们用来做线性回归梯度下降的。
那么,线性回归和逻辑回归是同一个算法吗?要回答这个问题,我们要观察逻辑回归看看发生了哪些变化。实际上,假设的定义发生了变化。
对于线性回归假设函数:
h θ ( x ) = θ T X = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n {h_\theta}\left( x \right)={\theta^T}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θTX=θ0x0+θ1x1+θ2x2+...+θnxn
而现在逻辑函数假设函数:
h θ ( x ) = 1 1 + e − θ T X {h_\theta}\left( x \right)=\frac{1}{1+{ {e}^{-{\theta^T}X}}} hθ(x)=1+e−θTX1
因此,即使更新参数的规则看起来基本相同,但由于假设的定义发生了变化,所以逻辑函数的梯度下降,跟线性回归的梯度下降实际上是两个完全不同的东西。
在先前的视频中,当我们在谈论线性回归的梯度下降法时,我们谈到了如何监控梯度下降法以确保其收敛,我通常也把同样的方法用在逻辑回归中,来监测梯度下降,以确保它正常收敛。
当使用梯度下降法来实现逻辑回归时,我们有这些不同的参数$\theta , 就 是 ,就是 ,就是{\theta_{0}}$ θ 1 {\theta_{1}} θ1 θ 2 {\theta_{2}} θ2 一直到 θ n {\theta_{n}} θn,我们需要用这个表达式来更新这些参数。我们还可以使用 for循环来更新这些参数值,用 for i=1 to n,或者 for i=1 to n+1。当然,不用 for循环也是可以的,理想情况下,我们更提倡使用向量化的实现,可以把所有这些 n n n个参数同时更新。
最后还有一点,我们之前在谈线性回归时讲到的特征缩放,我们看到了特征缩放是如何提高梯度下降的收敛速度的,这个特征缩放的方法,也适用于逻辑回归。如果你的特征范围差距很大的话,那么应用特征缩放的方法,同样也可以让逻辑回归中,梯度下降收敛更快。
就是这样,现在你知道如何实现逻辑回归,这是一种非常强大,甚至可能世界上使用最广泛的一种分类算法。
6.6 高级优化
使通过梯度下降,进行逻辑回归的速度大大提高,而这也将使算法更加适合解决大型的机器学习问题
假设我们已经完成了可以实现这两件事的代码,那么梯度下降所做的就是反复执行这些更新。 另一种考虑梯度下降的思路是:我们需要写出代码来计算 J ( θ ) J\left( \theta \right) J(θ) 和这些偏导数,然后把这些插入到梯度下降中,然后它就可以为我们最小化这个函数。 对于梯度下降来说,我认为从技术上讲,你实际并不需要编写代码来计算代价函数 J ( θ ) J\left( \theta \right) J(θ)。你只需要编写代码来计算导数项,但是,如果你希望代码还要能够监控这些 J ( θ ) J\left( \theta \right) J(θ) 的收敛性,那么我们就需要自己编写代码来计算代价函数 J ( θ ) J(\theta) J(θ)和偏导数项 ∂ ∂ θ j J ( θ ) \frac{\partial }{\partial {\theta_j}}J\left( \theta \right) ∂θj∂J(θ)。所以,在写完能够计算这两者的代码之后,我们就可以使用梯度下降。 然而梯度下降并不是我们可以使用的唯一算法,还有其他一些算法,更高级、更复杂。如果我们能用这些方法来计算代价函数 J ( θ ) J\left( \theta \right) J(θ)和偏导数项 ∂ ∂ θ j J ( θ ) \frac{\partial }{\partial {\theta_j}}J\left( \theta \right) ∂θj∂J(θ)两个项的话,那么这些算法就是为我们优化代价函数的不同方法,共轭梯度法 BFGS (变尺度法) 和L-BFGS (限制变尺度法) 就是其中一些更高级的优化算法,它们需要有一种方法来计算 J ( θ ) J\left( \theta \right) J(θ),以及需要一种方法计算导数项,然后使用比梯度下降更复杂的算法来最小化代价函数。这三种算法的具体细节超出了本门课程的范畴。实际上你最后通常会花费很多天,或几周时间研究这些算法,你可以专门学一门课来提高数值计算能力,不过让我来告诉你他们的一些特性:
这三种算法有许多优点:
一个是使用这其中任何一个算法,你通常不需要手动选择学习率 α \alpha α,所以对于这些算法的一种思路是,给出计算导数项和代价函数的方法,你可以认为算法有一个智能的内部循环,而且,事实上,他们确实有一个智能的内部循环,称为线性搜索(line search)算法,它可以自动尝试不同的学习速率 α \alpha α,并自动选择一个好的学习速率 a a a,因此它甚至可以为每次迭代选择不同的学习速率,那么你就不需要自己选择。这些算法实际上在做更复杂的事情,不仅仅是选择一个好的学习速率,所以它们往往最终比梯度下降收敛得快多了,不过关于它们到底做什么的详细讨论,已经超过了本门课程的范围。
6.7 多类别分类:一对多
如何使用逻辑回归 (logistic regression)来解决多类别分类问题,具体来说,我想通过一个叫做"一对多" (one-vs-all) 的分类算法。
我们先从用三角形代表的类别1开始,实际上我们可以创建一个,新的"伪"训练集,类型2和类型3定为负类,类型1设定为正类,我们创建一个新的训练集,如下图所示的那样,我们要拟合出一个合适的分类器。
最后,在我们需要做预测时,我们将所有的分类机都运行一遍,然后对每一个输入变量,都选择最高可能性的输出变量。
七、正则化(Regularization)
7.1 过拟合的问题(over-fitting)
如果我们发现了过拟合问题,应该如何处理?
- 丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如PCA)
- 正则化。 保留所有的特征,但是减少参数的大小(magnitude)。
7.2 代价函数
上面的回归问题中如果我们的模型是: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 2 + θ 3 x 3 3 + θ 4 x 4 4 {h_\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2}+{\theta_{3}}{x_{3}^3}+{\theta_{4}}{x_{4}^4} hθ(x)=θ0+θ1x1+θ2x22+θ3x33+θ4x44 我们可以从之前的事例中看出,正是那些高次项导致了过拟合的产生,所以如果我们能让这些高次项的系数接近于0的话,我们就能很好的拟合了。 所以我们要做的就是在一定程度上减小这些参数$\theta $ 的值,这就是正则化的基本方法。我们决定要减少 θ 3 {\theta_{3}} θ3和 θ 4 {\theta_{4}} θ4的大小,我们要做的便是修改代价函数,在其中 θ 3 {\theta_{3}} θ3和 θ 4 {\theta_{4}} θ4 设置一点惩罚。这样做的话,我们在尝试最小化代价时也需要将这个惩罚纳入考虑中,并最终导致选择较小一些的 θ 3 {\theta_{3}} θ3和 θ 4 {\theta_{4}} θ4。 修改后的代价函数如下: min θ , 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + 1000 θ 3 2 + 10000 θ 4 2 ] \underset{\theta }{\mathop{\min }},\frac{1}{2m}[\sum\limits_{i=1}^{m}{ { {\left( { {h}_{\theta }}\left( { {x}^{(i)}} \right)-{ {y}^{(i)}} \right)}^{2}}+1000\theta _{3}^{2}+10000\theta _{4}^{2}]} θmin,2m1[i=1∑m(hθ(x(i))−y(i))2+1000θ32+10000θ42]
通过这样的代价函数选择出的 θ 3 {\theta_{3}} θ3和 θ 4 {\theta_{4}} θ4 对预测结果的影响就比之前要小许多。假如我们有非常多的特征,我们并不知道其中哪些特征我们要惩罚,我们将对所有的特征进行惩罚,并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设: J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J\left( \theta \right)=\frac{1}{2m}[\sum\limits_{i=1}^{m}{ { {({h_\theta}({ {x}^{(i)}})-{ {y}^{(i)}})}^{2}}+\lambda \sum\limits_{j=1}^{n}{\theta_{j}^{2}}]} J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
其中$\lambda 又 称 为 正 则 化 参 数 ( ∗ ∗ R e g u l a r i z a t i o n P a r a m e t e r ∗ ∗ ) 。 注 : 根 据 惯 例 , 我 们 不 对 又称为正则化参数(**Regularization Parameter**)。 注:根据惯例,我们不对 又称为正则化参数(∗∗RegularizationParameter∗∗)。注:根据惯例,我们不对{\theta_{0}}$ 进行惩罚。经过正则化处理的模型与原模型的可能对比如下图所示:
如果选择的正则化参数 λ \lambda λ 过大,则会把所有的参数都最小化了,导致模型变成 h θ ( x ) = θ 0 {h_\theta}\left( x \right)={\theta_{0}} hθ(x)=θ0,也就是上图中红色直线所示的情况,造成欠拟合。 那为什么增加的一项 λ = ∑ j = 1 n θ j 2 \lambda =\sum\limits_{j=1}^{n}{\theta_j^{2}} λ=j=1∑nθj2 可以使$\theta $的值减小呢? 因为如果我们令 λ \lambda λ 的值很大的话,为了使Cost Function 尽可能的小,所有的 $\theta $ 的值(不包括 θ 0 {\theta_{0}} θ0)都会在一定程度上减小。 但若 λ \lambda λ 的值太大了,那么$\theta ( 不 包 括 (不包括 (不包括{\theta_{0}} ) 都 会 趋 近 于 0 , 这 样 我 们 所 得 到 的 只 能 是 一 条 平 行 于 )都会趋近于0,这样我们所得到的只能是一条平行于 )都会趋近于0,这样我们所得到的只能是一条平行于x$轴的直线。 所以对于正则化,我们要取一个合理的 λ \lambda λ 的值,这样才能更好的应用正则化。 回顾一下代价函数,为了使用正则化,让我们把这些概念应用到到线性回归和逻辑回归中去,那么我们就可以让他们避免过度拟合了。
7.3 正则化线性回归
对于线性回归的求解,我们之前推导了两种学习算法:一种基于梯度下降,一种基于正规方程。
正则化线性回归的代价函数为:
J ( θ ) = 1 2 m ∑ i = 1 m [ ( ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ) ] J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{[({ {({h_\theta}({ {x}^{(i)}})-{ {y}^{(i)}})}^{2}}+\lambda \sum\limits_{j=1}^{n}{\theta _{j}^{2}})]} J(θ)=2m1i=1∑m[((hθ(x(i))−y(i))2+λj=1∑nθj2)]
如果我们要使用梯度下降法令这个代价函数最小化,因为我们未对 θ 0 \theta_0 θ0进行正则化,所以梯度下降算法将分两种情形:
R e p e a t Repeat Repeat u n t i l until until c o n v e r g e n c e convergence convergence{
θ 0 : = θ 0 − a 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) ) {\theta_0}:={\theta_0}-a\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({ {x}^{(i)}})-{ {y}^{(i)}})x_{0}^{(i)}}) θ0:=θ0−am1i=1∑m((hθ(x(i))−y(i))x0(i))
θ j : = θ j − a [ 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] {\theta_j}:={\theta_j}-a[\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({ {x}^{(i)}})-{ {y}^{(i)}})x_{j}^{\left( i \right)}}+\frac{\lambda }{m}{\theta_j}] θj:=θj−a[m1i=1∑m((hθ(x(i))−y(i))xj(i)+mλθj]
f o r for for j = 1 , 2 , . . . n j=1,2,...n j=1,2,...n
}
对上面的算法中$ j=1,2,…,n$ 时的更新式子进行调整可得:
θ j : = θ j ( 1 − a λ m ) − a 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) {\theta_j}:={\theta_j}(1-a\frac{\lambda }{m})-a\frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({ {x}^{(i)}})-{ {y}^{(i)}})x_{j}^{\left( i \right)}} θj:=θj(1−amλ)−am1i=1∑m(hθ(x(i))−y(i))xj(i) 可以看出,正则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令$\theta $值减少了一个额外的值。
我们同样也可以利用正规方程来求解正则化线性回归模型
7.4 正则化的逻辑回归模型
针对逻辑回归问题,我们在之前的课程已经学习过两种优化算法:我们首先学习了使用梯度下降法来优化代价函数 J ( θ ) J\left( \theta \right) J(θ),接下来学习了更高级的优化算法,这些高级优化算法需要你自己设计代价函数 J ( θ ) J\left( \theta \right) J(θ)。
自己计算导数同样对于逻辑回归,我们也给代价函数增加一个正则化的表达式,得到代价函数:
J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{ {y}^{(i)}}\log \left( {h_\theta}\left( { {x}^{(i)}} \right) \right)-\left( 1-{ {y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( { {x}^{(i)}} \right) \right)]}+\frac{\lambda }{2m}\sum\limits_{j=1}^{n}{\theta _{j}^{2}} J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
要最小化该代价函数,通过求导,得出梯度下降算法为:
R e p e a t Repeat Repeat u n t i l until until c o n v e r g e n c e convergence convergence{
θ 0 : = θ 0 − a 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) ) {\theta_0}:={\theta_0}-a\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({ {x}^{(i)}})-{ {y}^{(i)}})x_{0}^{(i)}}) θ0:=θ0−am1i=1∑m((hθ(x(i))−y(i))x0(i))
θ j : = θ j − a [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] {\theta_j}:={\theta_j}-a[\frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({ {x}^{(i)}})-{ {y}^{(i)}})x_{j}^{\left( i \right)}}+\frac{\lambda }{m}{\theta_j}] θj:=θj−a[m1i=1∑m(hθ(x(i))−y(i))xj(i)+mλθj]
f o r for for j = 1 , 2 , . . . n j=1,2,...n j=1,2,...n
}
注:看上去同线性回归一样,但是知道 h θ ( x ) = g ( θ T X ) {h_\theta}\left( x \right)=g\left( {\theta^T}X \right) hθ(x)=g(θTX),所以与线性回归不同。 Octave 中,我们依旧可以用 fminuc 函数来求解代价函数最小化的参数,值得注意的是参数 θ 0 {\theta_{0}} θ0的更新规则与其他情况不同。 注意:
- 虽然正则化的逻辑回归中的梯度下降和正则化的线性回归中的表达式看起来一样,但由于两者的 h θ ( x ) {h_\theta}\left( x \right) hθ(x)不同所以还是有很大差别。
- θ 0 {\theta_{0}} θ0不参与其中的任何一个正则化。
神经网络:表述(Neural Networks: Representation)
8.1 非线性假设
我们之前学的,无论是线性回归还是逻辑回归都有这样一个缺点,即:当特征太多时,计算的负荷会非常大。
普通的逻辑回归模型,不能有效地处理这么多的特征,这时候我们需要神经网络。
8.2 神经元和大脑
神经网络是一种很古老的算法,它最初产生的目的是制造能模拟大脑的机器。
8.3 模型表示1
为了构建神经网络模型,我们需要首先思考大脑中的神经网络是怎样的?每一个神经元都可以被认为是一个处理单元/神经核(processing unit/Nucleus),它含有许多输入/树突(input/Dendrite),并且有一个输出/轴突(output/Axon)。神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络。
神经网络模型建立在很多神经元之上,每一个神经元又是一个个学习模型。这些神经元(也叫激活单元,activation unit)采纳一些特征作为输出,并且根据本身的模型提供一个输出。下图是一个以逻辑回归模型作为自身学习模型的神经元示例,在神经网络中,参数又可被称为权重(weight)。
神经网络模型是许多逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。下图为一个3层的神经网络,第一层成为输入层(Input Layer),最后一层称为输出层(Output Layer),中间一层成为隐藏层(Hidden Layers)。我们为每一层都增加一个偏差单位(bias unit):
下面引入一些标记法来帮助描述模型: a i ( j ) a_{i}^{\left( j \right)} ai(j) 代表第 j j j 层的第 i i i 个激活单元。 θ ( j ) { {\theta }^{\left( j \right)}} θ(j)代表从第 j j j 层映射到第$ j+1$ 层时的权重的矩阵,例如 θ ( 1 ) { {\theta }^{\left( 1 \right)}} θ(1)代表从第一层映射到第二层的权重的矩阵。其尺寸为:以第 j + 1 j+1 j+1层的激活单元数量为行数,以第 j j j 层的激活单元数加一为列数的矩阵。例如:上图所示的神经网络中 θ ( 1 ) { {\theta }^{\left( 1 \right)}} θ(1)的尺寸为 3*4。
对于上图所示的模型,激活单元和输出分别表达为:
a 1 ( 2 ) = g ( Θ ∗ 10 ( 1 ) x ∗ 0 + Θ ∗ 11 ( 1 ) x ∗ 1 + Θ ∗ 12 ( 1 ) x ∗ 2 + Θ ∗ 13 ( 1 ) x ∗ 3 ) a_{1}^{(2)}=g(\Theta *{10}^{(1)}{ {x}*{0}}+\Theta *{11}^{(1)}{ {x}*{1}}+\Theta *{12}^{(1)}{ {x}*{2}}+\Theta *{13}^{(1)}{ {x}*{3}}) a1(2)=g(Θ∗10(1)x∗0+Θ∗11(1)x∗1+Θ∗12(1)x∗2+Θ∗13(1)x∗3) a 2 ( 2 ) = g ( Θ ∗ 20 ( 1 ) x ∗ 0 + Θ ∗ 21 ( 1 ) x ∗ 1 + Θ ∗ 22 ( 1 ) x ∗ 2 + Θ ∗ 23 ( 1 ) x ∗ 3 ) a_{2}^{(2)}=g(\Theta *{20}^{(1)}{ {x}*{0}}+\Theta *{21}^{(1)}{ {x}*{1}}+\Theta *{22}^{(1)}{ {x}*{2}}+\Theta *{23}^{(1)}{ {x}*{3}}) a2(2)=g(Θ∗20(1)x∗0+Θ∗21(1)x∗1+Θ∗22(1)x∗2+Θ∗23(1)x∗3) a 3 ( 2 ) = g ( Θ ∗ 30 ( 1 ) x ∗ 0 + Θ ∗ 31 ( 1 ) x ∗ 1 + Θ ∗ 32 ( 1 ) x ∗ 2 + Θ ∗ 33 ( 1 ) x ∗ 3 ) a_{3}^{(2)}=g(\Theta *{30}^{(1)}{ {x}*{0}}+\Theta *{31}^{(1)}{ {x}*{1}}+\Theta *{32}^{(1)}{ {x}*{2}}+\Theta *{33}^{(1)}{ {x}*{3}}) a3(2)=g(Θ∗30(1)x∗0+Θ∗31(1)x∗1+Θ∗32(1)x∗2+Θ∗33(1)x∗3) h Θ ( x ) = g ( Θ ∗ 10 ( 2 ) a ∗ 0 ( 2 ) + Θ ∗ 11 ( 2 ) a ∗ 1 ( 2 ) + Θ ∗ 12 ( 2 ) a ∗ 2 ( 2 ) + Θ ∗ 13 ( 2 ) a ∗ 3 ( 2 ) ) { {h}_{\Theta }}(x)=g(\Theta *{10}^{(2)}a*{0}^{(2)}+\Theta *{11}^{(2)}a*{1}^{(2)}+\Theta *{12}^{(2)}a*{2}^{(2)}+\Theta *{13}^{(2)}a*{3}^{(2)}) hΘ(x)=g(Θ∗10(2)a∗0(2)+Θ∗11(2)a∗1(2)+Θ∗12(2)a∗2(2)+Θ∗13(2)a∗3(2))
上面进行的讨论中只是将特征矩阵中的一行(一个训练实例)喂给了神经网络,我们需要将整个训练集都喂给我们的神经网络算法来学习模型。
我们可以知道:每一个 a a a都是由上一层所有的 x x x和每一个 x x x所对应的决定的。
(我们把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION ))
我们可以得到 θ ⋅ X = a \theta \cdot X=a θ⋅X=a 。
8.4 模型表示2
( FORWARD PROPAGATION ) 相对于使用循环来编码,利用向量化的方法会使得计算更为简便。
我们令 z ( 3 ) = θ ( 2 ) a ( 2 ) { {z}^{\left( 3 \right)}}={ {\theta }^{\left( 2 \right)}}{ {a}^{\left( 2 \right)}} z(3)=θ(2)a(2),则 h θ ( x ) = a ( 3 ) = g ( z ( 3 ) ) h_\theta(x)={ {a}^{\left( 3 \right)}}=g({ {z}^{\left( 3 \right)}}) hθ(x)=a(3)=g(z(3))。 这只是针对训练集中一个训练实例所进行的计算。如果我们要对整个训练集进行计算,我们需要将训练集特征矩阵进行转置,使得同一个实例的特征都在同一列里。即: ${ {z}^{\left( 2 \right)}}={ {\Theta }^{\left( 1 \right)}}\times { {X}^{T}} $
a ( 2 ) = g ( z ( 2 ) ) { {a}^{\left( 2 \right)}}=g({ {z}^{\left( 2 \right)}}) a(2)=g(z(2))
其实神经网络就像是logistic regression,只不过我们把logistic regression中的输入向量 [ x 1 ∼ x 3 ] \left[ x_1\sim {x_3} \right] [x1∼x3] 变成了中间层的 [ a 1 ( 2 ) ∼ a 3 ( 2 ) ] \left[ a_1^{(2)}\sim a_3^{(2)} \right] [a1(2)∼a3(2)], 即: h θ ( x ) = g ( Θ 0 ( 2 ) a 0 ( 2 ) + Θ 1 ( 2 ) a 1 ( 2 ) + Θ 2 ( 2 ) a 2 ( 2 ) + Θ 3 ( 2 ) a 3 ( 2 ) ) h_\theta(x)=g\left( \Theta_0^{\left( 2 \right)}a_0^{\left( 2 \right)}+\Theta_1^{\left( 2 \right)}a_1^{\left( 2 \right)}+\Theta_{2}^{\left( 2 \right)}a_{2}^{\left( 2 \right)}+\Theta_{3}^{\left( 2 \right)}a_{3}^{\left( 2 \right)} \right) hθ(x)=g(Θ0(2)a0(2)+Θ1(2)a1(2)+Θ2(2)a2(2)+Θ3(2)a3(2)) 我们可以把 a 0 , a 1 , a 2 , a 3 a_0, a_1, a_2, a_3 a0,a1,a2,a3看成更为高级的特征值,也就是 x 0 , x 1 , x 2 , x 3 x_0, x_1, x_2, x_3 x0,x1,x2,x3的进化体,并且它们是由 x x x与 θ \theta θ决定的,因为是梯度下降的,所以 a a a是变化的,并且变得越来越厉害,所以这些更高级的特征值远比仅仅将 x x x次方厉害,也能更好的预测新数据。 这就是神经网络相比于逻辑回归和线性回归的优势。
8.5 特征和直观理解1
OR与AND整体一样,区别只在于的取值不同。
8.6 样本和直观理解II
二元逻辑运算符(BINARY LOGICAL OPERATORS)当输入特征为布尔值(0或1)时,我们可以用一个单一的激活层可以作为二元逻辑运算符,为了表示不同的运算符,我们只需要选择不同的权重即可。
8.7 多类分类
输入向量 x x x有三个维度,两个中间层,输出层4个神经元分别用来表示4类,也就是每一个数据在输出层都会出现 [ a b c d ] T { {\left[ a\text{ }b\text{ }c\text{ }d \right]}^{T}} [a b c d]T,且 a , b , c , d a,b,c,d a,b,c,d中仅有一个为1,表示当前类。
神经网络的学习(Neural Networks: Learning)
9.1 代价函数
首先引入一些便于稍后讨论的新标记方法:
假设神经网络的训练样本有 m m m个,每个包含一组输入 x x x和一组输出信号 y y y, L L L表示神经网络层数, S I S_I SI表示每层的neuron个数( S l S_l Sl表示输出层神经元个数), S L S_L SL代表最后一层中处理单元的个数。
将神经网络的分类定义为两种情况:二类分类和多类分类,
二类分类: S L = 1 , y = 0 , o r , 1 S_L=1, y=0, or, 1 SL=1,y=0,or,1表示哪一类;
K K K类分类: S L = k , y i = 1 S_L=k, y_i = 1 SL=k,yi=1表示分到第 i i i类; ( k > 2 ) (k>2) (k>2)
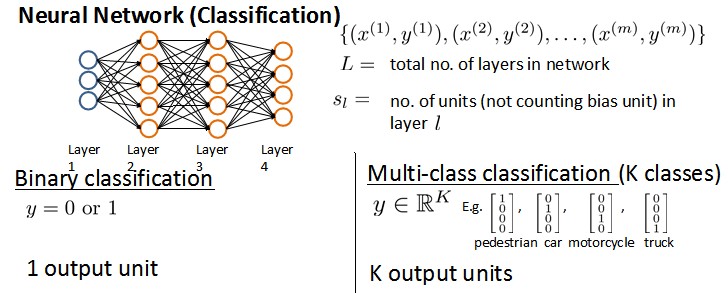
我们回顾逻辑回归问题中我们的代价函数为:
$ J\left(\theta \right)=-\frac{1}{m}\left[\sum_\limits{i=1}{m}{y}{(i)}\log{h_\theta({x}{(i)})}+\left(1-{y}{(i)}\right)log\left(1-h_\theta\left({x}{(i)}\right)\right)\right]+\frac{\lambda}{2m}\sum_\limits{j=1}{n}{\theta_j}^{2} $
在逻辑回归中,我们只有一个输出变量,又称标量(scalar),也只有一个因变量 y y y,但是在神经网络中,我们可以有很多输出变量,我们的 h θ ( x ) h_\theta(x) hθ(x)是一个维度为 K K K的向量,并且我们训练集中的因变量也是同样维度的一个向量,因此我们的代价函数会比逻辑回归更加复杂一些,为: \newcommand{\subk}[1]{ #1_k } h θ ( x ) ∈ R K h_\theta\left(x\right)\in \mathbb{R}^{K} hθ(x)∈RK ( h θ ( x ) ) i = i t h output {\left({h_\theta}\left(x\right)\right)}_{i}={i}^{th} \text{output} (hθ(x))i=ithoutput
KaTeX parse error: Undefined control sequence: \subk at position 94: …_k}^{(i)} \log \̲s̲u̲b̲k̲{(h_\Theta(x^{(…
这个看起来复杂很多的代价函数背后的思想还是一样的,我们希望通过代价函数来观察算法预测的结果与真实情况的误差有多大,唯一不同的是,对于每一行特征,我们都会给出 K K K个预测,基本上我们可以利用循环,对每一行特征都预测 K K K个不同结果,然后在利用循环在 K K K个预测中选择可能性最高的一个,将其与 y y y中的实际数据进行比较。
正则化的那一项只是排除了每一层 θ 0 \theta_0 θ0后,每一层的 θ \theta θ 矩阵的和。最里层的循环 j j j循环所有的行(由 s l + 1 s_{l+1} sl+1 层的激活单元数决定),循环 i i i则循环所有的列,由该层( s l s_l sl层)的激活单元数所决定。即: h θ ( x ) h_\theta(x) hθ(x)与真实值之间的距离为每个样本-每个类输出的加和,对参数进行regularization的bias项处理所有参数的平方和。
9.2 反向传播算法
之前我们在计算神经网络预测结果的时候我们采用了一种正向传播方法,我们从第一层开始正向一层一层进行计算,直到最后一层的 h θ ( x ) h_{\theta}\left(x\right) hθ(x)。
现在,为了计算代价函数的偏导数 ∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial\Theta^{(l)}_{ij}}J\left(\Theta\right) ∂Θij(l)∂J(Θ),我们需要采用一种反向传播算法,也就是首先计算最后一层的误差,然后再一层一层反向求出各层的误差,直到倒数第二层。 以一个例子来说明反向传播算法。
我们从最后一层的误差开始计算,误差是激活单元的预测( a ( 4 ) {a^{(4)}} a(4))与实际值( y k y^k yk)之间的误差,( k = 1 : k k=1:k k=1:k)。
我们用 δ \delta δ来表示误差,则: δ ( 4 ) = a ( 4 ) − y \delta^{(4)}=a^{(4)}-y δ(4)=a(4)−y
我们利用这个误差值来计算前一层的误差: δ ( 3 ) = ( Θ ( 3 ) ) T δ ( 4 ) ∗ g ′ ( z ( 3 ) ) \delta^{(3)}=\left({\Theta^{(3)}}\right)^{T}\delta^{(4)}\ast g'\left(z^{(3)}\right) δ(3)=(Θ(3))Tδ(4)∗g′(z(3))
其中 g ′ ( z ( 3 ) ) g'(z^{(3)}) g′(z(3))是 S S S 形函数的导数, g ′ ( z ( 3 ) ) = a ( 3 ) ∗ ( 1 − a ( 3 ) ) g'(z^{(3)})=a^{(3)}\ast(1-a^{(3)}) g′(z(3))=a(3)∗(1−a(3))。而 ( θ ( 3 ) ) T δ ( 4 ) (θ^{(3)})^{T}\delta^{(4)} (θ(3))Tδ(4)则是权重导致的误差的和。下一步是继续计算第二层的误差:
$ \delta{(2)}=(\Theta{(2)}){T}\delta{(3)}\ast g’(z^{(2)})$
因为第一层是输入变量,不存在误差。我们有了所有的误差的表达式后,便可以计算代价函数的偏导数了,假设 λ = 0 λ=0 λ=0,即我们不做任何正则化处理时有:
∂ ∂ Θ i j ( l ) J ( Θ ) = a j ( l ) δ i l + 1 \frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)=a_{j}^{(l)} \delta_{i}^{l+1} ∂Θij(l)∂J(Θ)=aj(l)δil+1
重要的是清楚地知道上面式子中上下标的含义:
l l l 代表目前所计算的是第几层。
j j j 代表目前计算层中的激活单元的下标,也将是下一层的第 j j j个输入变量的下标。
i i i 代表下一层中误差单元的下标,是受到权重矩阵中第 i i i行影响的下一层中的误差单元的下标。
如果我们考虑正则化处理,并且我们的训练集是一个特征矩阵而非向量。在上面的特殊情况中,我们需要计算每一层的误差单元来计算代价函数的偏导数。在更为一般的情况中,我们同样需要计算每一层的误差单元,但是我们需要为整个训练集计算误差单元,此时的误差单元也是一个矩阵,我们用 Δ i j ( l ) \Delta^{(l)}_{ij} Δij(l)来表示这个误差矩阵。第 l l l 层的第 i i i 个激活单元受到第 j j j 个参数影响而导致的误差。
我们的算法表示为:

即首先用正向传播方法计算出每一层的激活单元,利用训练集的结果与神经网络预测的结果求出最后一层的误差,然后利用该误差运用反向传播法计算出直至第二层的所有误差。
在求出了 Δ i j ( l ) \Delta_{ij}^{(l)} Δij(l)之后,我们便可以计算代价函数的偏导数了,计算方法如下:
$ D_{ij}^{(l)} :=\frac{1}{m}\Delta_{ij}{(l)}+\lambda\Theta_{ij}{(l)}$ i f j ≠ 0 {if}\; j \neq 0 ifj=0
$ D_{ij}^{(l)} :=\frac{1}{m}\Delta_{ij}^{(l)}$ i f j = 0 {if}\; j = 0 ifj=0
9.3 反向传播算法的直观理解
感悟:上图中的 δ j ( l ) = " e r r o r " o f c o s t f o r a j ( l ) ( u n i t j i n l a y e r l ) \delta^{(l)}_{j}="error" \ of cost \ for \ a^{(l)}_{j} \ (unit \ j \ in \ layer \ l) δj(l)="error" ofcost for aj(l) (unit j in layer l) 理解如下:
δ j ( l ) \delta^{(l)}_{j} δj(l) 相当于是第 l l l 层的第 j j j 单元中得到的激活项的“误差”,即”正确“的 a j ( l ) a^{(l)}_{j} aj(l) 与计算得到的 a j ( l ) a^{(l)}_{j} aj(l) 的差。
而 a j ( l ) = g ( z ( l ) ) a^{(l)}_{j}=g(z^{(l)}) aj(l)=g(z(l)) ,(g为sigmoid函数)。我们可以想象 δ j ( l ) \delta^{(l)}_{j} δj(l) 为函数求导时迈出的那一丁点微分,所以更准确的说 δ j ( l ) = ∂ ∂ z j ( l ) c o s t ( i ) \delta^{(l)}_{j}=\frac{\partial}{\partial z^{(l)}_{j}}cost(i) δj(l)=∂zj(l)∂cost(i)
9.4 实现注意:展开参数
9.5 梯度检验
当我们对一个较为复杂的模型(例如神经网络)使用梯度下降算法时,可能会存在一些不容易察觉的错误,意味着,虽然代价看上去在不断减小,但最终的结果可能并不是最优解。
为了避免这样的问题,我们采取一种叫做梯度的数值检验(Numerical Gradient Checking)方法。这种方法的思想是通过估计梯度值来检验我们计算的导数值是否真的是我们要求的。
对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。即对于某个特定的 θ \theta θ,我们计算出在 θ \theta θ-$\varepsilon $ 处和 θ \theta θ+$\varepsilon $ 的代价值($\varepsilon $是一个非常小的值,通常选取 0.001),然后求两个代价的平均,用以估计在 θ \theta θ 处的代价值。
当 θ \theta θ是一个向量时,我们则需要对偏导数进行检验。因为代价函数的偏导数检验只针对一个参数的改变进行检验,下面是一个只针对 θ 1 \theta_1 θ1进行检验的示例:
∂ ∂ θ 1 = J ( θ 1 + ε 1 , θ 2 , θ 3 . . . θ n ) − J ( θ 1 − ε 1 , θ 2 , θ 3 . . . θ n ) 2 ε \frac{\partial}{\partial\theta_1}=\frac{J\left(\theta_1+\varepsilon_1,\theta_2,\theta_3...\theta_n \right)-J \left( \theta_1-\varepsilon_1,\theta_2,\theta_3...\theta_n \right)}{2\varepsilon} ∂θ1∂=2εJ(θ1+ε1,θ2,θ3...θn)−J(θ1−ε1,θ2,θ3...θn)
最后我们还需要对通过反向传播方法计算出的偏导数进行检验。
根据上面的算法,计算出的偏导数存储在矩阵 D i j ( l ) D_{ij}^{(l)} Dij(l) 中。检验时,我们要将该矩阵展开成为向量,同时我们也将 θ \theta θ 矩阵展开为向量,我们针对每一个 θ \theta θ 都计算一个近似的梯度值,将这些值存储于一个近似梯度矩阵中,最终将得出的这个矩阵同 D i j ( l ) D_{ij}^{(l)} Dij(l) 进行比较。
9.6 随机初始化
任何优化算法都需要一些初始的参数。到目前为止我们都是初始所有参数为0,这样的初始方法对于逻辑回归来说是可行的,但是对于神经网络来说是不可行的。如果我们令所有的初始参数都为0,这将意味着我们第二层的所有激活单元都会有相同的值。同理,如果我们初始所有的参数都为一个非0的数,结果也是一样的。
我们通常初始参数为正负ε之间的随机值
9.7 综合起来
我们真正要决定的是隐藏层的层数和每个中间层的单元数。
训练神经网络:
-
参数的随机初始化
-
利用正向传播方法计算所有的 h θ ( x ) h_{\theta}(x) hθ(x)
-
编写计算代价函数 J J J 的代码
-
利用反向传播方法计算所有偏导数
-
利用数值检验方法检验这些偏导数
-
使用优化算法来最小化代价函数
9.8 自主驾驶
这就是基于神经网络的自动驾驶技术。当然,我们还有很多更加先进的试验来实现自动驾驶技术。在美国,欧洲等一些国家和地区,他们提供了一些比这个方法更加稳定的驾驶控制技术。但我认为,使用这样一个简单的基于反向传播的神经网络,训练出如此强大的自动驾驶汽车,的确是一次令人惊讶的成就。
应用机器学习的建议(Advice for Applying Machine Learning)
10.1 决定下一步做什么
当我们运用训练好了的模型来预测未知数据的时候发现有较大的误差,我们下一步可以做什么?
-
获得更多的训练样本——通常是有效的,但代价较大,下面的方法也可能有效,可考虑先采用下面的几种方法。
-
尝试减少特征的数量
-
尝试获得更多的特征
-
尝试增加多项式特征
-
尝试减少正则化程度 λ \lambda λ
-
尝试增加正则化程度 λ \lambda λ
我们不应该随机选择上面的某种方法来改进我们的算法,而是运用一些机器学习诊断法来帮助我们知道上面哪些方法对我们的算法是有效的。
10.2 评估一个假设
为了检验算法是否过拟合,我们将数据分成训练集和测试集,通常用70%的数据作为训练集,用剩下30%的数据作为测试集。很重要的一点是训练集和测试集均要含有各种类型的数据,通常我们要对数据进行“洗牌”,然后再分成训练集和测试集。
测试集评估在通过训练集让我们的模型学习得出其参数后,对测试集运用该模型,我们有两种方式计算误差:
- 对于线性回归模型,我们利用测试集数据计算代价函数 J J J
- 对于逻辑回归模型,我们除了可以利用测试数据集来计算代价函数外:
KaTeX parse error: Expected group after '_' at position 48: …{m}_{test}}\sum_̲\limits{i=1}^{m…
误分类的比率,对于每一个测试集样本,计算:
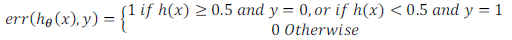
然后对计算结果求平均。
10.3 模型选择和交叉验证集
适应训练数据集并不代表着能推广至一般情况,我们应该选择一个更能适应一般情况的模型。我们需要使用交叉验证集来帮助选择模型。
即:使用60%的数据作为训练集,使用 20%的数据作为交叉验证集,使用20%的数据作为测试集
模型选择的方法为:
-
使用训练集训练出10个模型
-
用10个模型分别对交叉验证集计算得出交叉验证误差(代价函数的值)
-
选取代价函数值最小的模型
-
用步骤3中选出的模型对测试集计算得出推广误差(代价函数的值)
-
Train/validation/test error
Training error:
KaTeX parse error: Expected group after '_' at position 37: …frac{1}{2m}\sum_̲\limits{i=1}^{m…
Cross Validation error:
KaTeX parse error: Expected group after '_' at position 39: …1}{2m_{cv}}\sum_̲\limits{i=1}^{m…
Test error:
KaTeX parse error: Expected group after '_' at position 41: …{2m_{test}}\sum_̲\limits{i=1}^{m…
10.4 诊断偏差和方差
训练集误差和交叉验证集误差近似时:偏差/欠拟合
交叉验证集误差远大于训练集误差时:方差/过拟合
10.5 正则化和偏差/方差
我们选择一系列的想要测试的 λ \lambda λ 值,通常是 0-10之间的呈现2倍关系的值(如: 0 , 0.01 , 0.02 , 0.04 , 0.08 , 0.15 , 0.32 , 0.64 , 1.28 , 2.56 , 5.12 , 10 0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10 0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10共12个)。 我们同样把数据分为训练集、交叉验证集和测试集。
选择 λ \lambda λ的方法为:
- 使用训练集训练出12个不同程度正则化的模型
- 用12个模型分别对交叉验证集计算的出交叉验证误差
- 选择得出交叉验证误差最小的模型
- 运用步骤3中选出模型对测试集计算得出推广误差,我们也可以同时将训练集和交叉验证集模型的代价函数误差与λ的值绘制在一张图表上:
• 当 λ \lambda λ 较小时,训练集误差较小(过拟合)而交叉验证集误差较大
• 随着 λ \lambda λ 的增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增加
10.6 学习曲线
学习曲线就是一种很好的工具,我经常使用学习曲线来判断某一个学习算法是否处于偏差、方差问题。学习曲线是学习算法的一个很好的合理检验(sanity check)。学习曲线是将训练集误差和交叉验证集误差作为训练集样本数量( m m m)的函数绘制的图表。
如何利用学习曲线识别高偏差/欠拟合:作为例子,我们尝试用一条直线来适应下面的数据,可以看出,无论训练集有多么大误差都不会有太大改观:
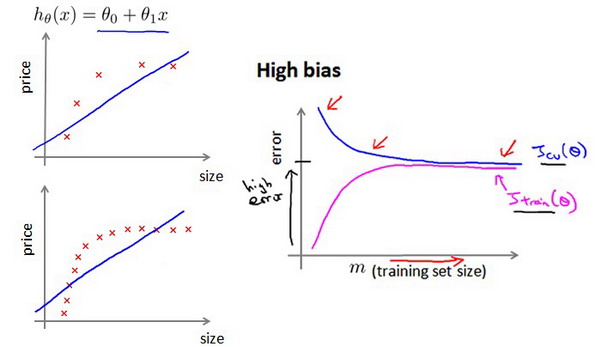
也就是说在高偏差/欠拟合的情况下,增加数据到训练集不一定能有帮助。
如何利用学习曲线识别高方差/过拟合:假设我们使用一个非常高次的多项式模型,并且正则化非常小,可以看出,当交叉验证集误差远大于训练集误差时,往训练集增加更多数据可以提高模型的效果。
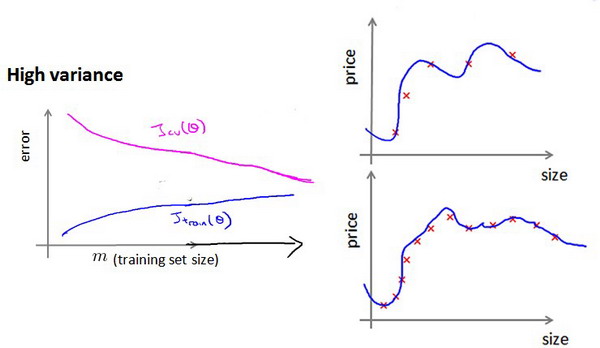
也就是说在高方差/过拟合的情况下,增加更多数据到训练集可能可以提高算法效果。
10.7 决定下一步做什么
哪些方法可能有助于改进学习算法的效果,而哪些可能是徒劳的呢?
回顾 1.1 中提出的六种可选的下一步,让我们来看一看我们在什么情况下应该怎样选择:
-
获得更多的训练样本——解决高方差
-
尝试减少特征的数量——解决高方差
-
尝试获得更多的特征——解决高偏差
-
尝试增加多项式特征——解决高偏差
-
尝试减少正则化程度λ——解决高偏差
-
尝试增加正则化程度λ——解决高方差
使用较小的神经网络,类似于参数较少的情况,容易导致高偏差和欠拟合,但计算代价较小使用较大的神经网络,类似于参数较多的情况,容易导致高方差和过拟合,虽然计算代价比较大,但是可以通过正则化手段来调整而更加适应数据。
对于神经网络中的隐藏层的层数的选择,通常从一层开始逐渐增加层数,为了更好地作选择,可以把数据分为训练集、交叉验证集和测试集,针对不同隐藏层层数的神经网络训练神经网络,
然后选择交叉验证集代价最小的神经网络。
第3天
机器学习系统的设计(Machine Learning System Design)
11.1 首先要做什么
以一个垃圾邮件分类器算法为例进行讨论。
为了解决这样一个问题,我们首先要做的决定是如何选择并表达特征向量 x x x。我们可以选择一个由100个最常出现在垃圾邮件中的词所构成的列表,根据这些词是否有在邮件中出现,来获得我们的特征向量(出现为1,不出现为0),尺寸为100×1。
为了构建这个分类器算法,我们可以做很多事,例如:
-
收集更多的数据,让我们有更多的垃圾邮件和非垃圾邮件的样本
-
基于邮件的路由信息开发一系列复杂的特征
-
基于邮件的正文信息开发一系列复杂的特征,包括考虑截词的处理
-
为探测刻意的拼写错误(把watch 写成w4tch)开发复杂的算法
11.2 误差分析
误差分析(Error Analysis)的概念。这会帮助你更系统地做出决定。如果你准备研究机器学习的东西,或者构造机器学习应用程序,最好的实践方法不是建立一个非常复杂的系统,拥有多么复杂的变量;而是构建一个简单的算法,这样你可以很快地实现它。
构建一个学习算法的推荐方法为:
- 从一个简单的能快速实现的算法开始,实现该算法并用交叉验证集数据测试这个算法
2.绘制学习曲线,决定是增加更多数据,或者添加更多特征,还是其他选择
3.进行误差分析:人工检查交叉验证集中我们算法中产生预测误差的样本,看看这些样本是否有某种系统化的趋势
11.3 类偏斜的误差度量
类偏斜情况表现为我们的训练集中有非常多的同一种类的样本,只有很少或没有其他类的样本。
查准率(Precision)和查全率(Recall) 我们将算法预测的结果分成四种情况:
1.正确肯定(True Positive,TP):预测为真,实际为真
2.正确否定(True Negative,TN):预测为假,实际为假
3.错误肯定(False Positive,FP):预测为真,实际为假
4.错误否定(False Negative,FN):预测为假,实际为真
则:查准率=TP/(TP+FP)。例,在所有我们预测有恶性肿瘤的病人中,实际上有恶性肿瘤的病人的百分比,越高越好。
查全率=TP/(TP+FN)。例,在所有实际上有恶性肿瘤的病人中,成功预测有恶性肿瘤的病人的百分比,越高越好。
这样,对于我们刚才那个总是预测病人肿瘤为良性的算法,其查全率是0。
| 预测值 | |||
|---|---|---|---|
| Positive | Negtive | ||
| 实际值 | Positive | TP | FN |
| Negtive | FP | TN |
11.4 查准率和查全率之间的权衡
我们希望有一个帮助我们选择这个阀值的方法。一种方法是计算F1 值(F1 Score),其计算公式为:
F 1 S c o r e : 2 P R P + R { {F}_{1}}Score:2\frac{PR}{P+R} F1Score:2P+RPR
我们选择使得F1值最高的阀值。
11.5 机器学习的数据
在一定的条件下,得到大量的数据并在某种类型的学习算法中进行训练,可以是一种有效的方法来获得一个具有良好性能的学习算法。
支持向量机(Support Vector Machines)
12.1 优化目标
与逻辑回归和神经网络相比,支持向量机,或者简称SVM,在学习复杂的非线性方程时提供了一种更为清晰,更加强大的方式。
12.2 大边界的直观理解
这就相当于在支持向量机中嵌入了一个额外的安全因子,或者说安全的间距因子。
支持向量机将会选择这个黑色的决策边界,相较于之前我用粉色或者绿色画的决策界。这条黑色的看起来好得多,黑线看起来是更稳健的决策界。在分离正样本和负样本上它显得的更好。数学上来讲,这是什么意思呢?这条黑线有更大的距离,这个距离叫做间距(margin)。
这个距离叫做支持向量机的间距,而这是支持向量机具有鲁棒性的原因,因为它努力用一个最大间距来分离样本。因此支持向量机有时被称为大间距分类器
关于大间距分类器,我想讲最后一点:我们将这个大间距分类器中的正则化因子常数 C C C设置的非常大,我记得我将其设置为了100000,因此对这样的一个数据集,也许我们将选择这样的决策界,从而最大间距地分离开正样本和负样本。那么在让代价函数最小化的过程中,我们希望找出在 y = 1 y=1 y=1和 y = 0 y=0 y=0两种情况下都使得代价函数中左边的这一项尽量为零的参数。如果我们找到了这样的参数,则我们的最小化问题便转变成:
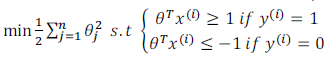
事实上,支持向量机现在要比这个大间距分类器所体现得更成熟,尤其是当你使用大间距分类器的时候,你的学习算法会受异常点(outlier) 的影响。比如我们加入一个额外的正样本。
当 C C C不是非常非常大的时候,它可以忽略掉一些异常点的影响,得到更好的决策界。
回顾 C = 1 / λ C=1/\lambda C=1/λ,因此:
C C C 较大时,相当于 λ \lambda λ 较小,可能会导致过拟合,高方差。
C C C 较小时,相当于 λ \lambda λ较大,可能会导致低拟合,高偏差。
12.3 大边界分类背后的数学(选修)
因此支持向量机做的全部事情,就是极小化参数向量 θ { {\theta }} θ范数的平方,或者说长度的平方。
12.4 核函数1
给定一个训练样本 x x x,我们利用 x x x的各个特征与我们预先选定的地标(landmarks) l ( 1 ) , l ( 2 ) , l ( 3 ) l^{(1)},l^{(2)},l^{(3)} l(1),l(2),l(3)的近似程度来选取新的特征 f 1 , f 2 , f 3 f_1,f_2,f_3 f1,f2,f3。
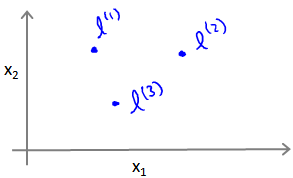
例如: f 1 = s i m i l a r i t y ( x , l ( 1 ) ) = e ( − ∥ x − l ( 1 ) ∥ 2 2 σ 2 ) { {f}_{1}}=similarity(x,{ {l}^{(1)}})=e(-\frac{ { {\left\| x-{ {l}^{(1)}} \right\|}^{2}}}{2{ {\sigma }^{2}}}) f1=similarity(x,l(1))=e(−2σ2∥x−l(1)∥2)
其中: ∥ x − l ( 1 ) ∥ 2 = ∑ j = 1 n ( x j − l j ( 1 ) ) 2 { {\left\| x-{ {l}^{(1)}} \right\|}^{2}}=\sum{_{j=1}^{n}}{ {({ {x}_{j}}-l_{j}^{(1)})}^{2}} ∥∥x−l(1)∥∥2=∑j=1n(xj−lj(1))2,为实例 x x x中所有特征与地标 l ( 1 ) l^{(1)} l(1)之间的距离的和。上例中的 s i m i l a r i t y ( x , l ( 1 ) ) similarity(x,{ {l}^{(1)}}) similarity(x,l(1))就是核函数,具体而言,这里是一个高斯核函数(Gaussian Kernel)。 注:这个函数与正态分布没什么实际上的关系,只是看上去像而已。
这些地标的作用是什么?如果一个训练样本 x x x与地标 l l l之间的距离近似于0,则新特征 f f f近似于 e − 0 = 1 e^{-0}=1 e−0=1,如果训练样本 x x x与地标 l l l之间距离较远,则 f f f近似于 e − ( 一 个 较 大 的 数 ) = 0 e^{-(一个较大的数)}=0 e−(一个较大的数)=0。
12.5 核函数2
如何选择地标?
我们通常是根据训练集的数量选择地标的数量,即如果训练集中有 m m m个样本,则我们选取 m m m个地标,并且令: l ( 1 ) = x ( 1 ) , l ( 2 ) = x ( 2 ) , . . . . . , l ( m ) = x ( m ) l^{(1)}=x^{(1)},l^{(2)}=x^{(2)},.....,l^{(m)}=x^{(m)} l(1)=x(1),l(2)=x(2),.....,l(m)=x(m)。这样做的好处在于:现在我们得到的新特征是建立在原有特征与训练集中所有其他特征之间距离的基础之上的
下面我们将核函数运用到支持向量机中,修改我们的支持向量机假设为:
• 给定 x x x,计算新特征 f f f,当 θ T f > = 0 θ^Tf>=0 θTf>=0 时,预测 y = 1 y=1 y=1,否则反之。
相应地修改代价函数为:$\sum{_{j=1}^{n=m}}\theta _{j}{2}={ {\theta}{T}}\theta $,
m i n C ∑ i = 1 m [ y ( i ) c o s t 1 ( θ T f ( i ) ) + ( 1 − y ( i ) ) c o s t 0 ( θ T f ( i ) ) ] + 1 2 ∑ j = 1 n = m θ j 2 min C\sum\limits_{i=1}^{m}{[{
{y}^{(i)}}cos {
{t}_{1}}}( {
{\theta }^{T}}{
{f}^{(i)}})+(1-{
{y}^{(i)}})cos {
{t}_{0}}( {
{\theta }^{T}}{
{f}^{(i)}})]+\frac{1}{2}\sum\limits_{j=1}^{n=m}{\theta _{j}^{2}} minCi=1∑m[y(i)cost1(θTf(i))+(1−y(i))cost0(θTf(i))]+21j=1∑n=mθj2
在具体实施过程中,我们还需要对最后的正则化项进行些微调整,在计算$\sum{_{j=1}^{n=m}}\theta _{j}{2}={
{\theta}{T}}\theta 时 , 我 们 用 时,我们用 时,我们用θTMθ$代替$θTθ , 其 中 ,其中 ,其中M$是根据我们选择的核函数而不同的一个矩阵。这样做的原因是为了简化计算。
理论上讲,我们也可以在逻辑回归中使用核函数,但是上面使用 M M M来简化计算的方法不适用与逻辑回归,因此计算将非常耗费时间。
下面是支持向量机的两个参数 C C C和 σ \sigma σ的影响:
C = 1 / λ C=1/\lambda C=1/λ
C C C 较大时,相当于 λ \lambda λ较小,可能会导致过拟合,高方差;
C C C 较小时,相当于 λ \lambda λ较大,可能会导致低拟合,高偏差;
σ \sigma σ较大时,可能会导致低方差,高偏差;
σ \sigma σ较小时,可能会导致低偏差,高方差。
12.6 使用支持向量机
在高斯核函数之外我们还有其他一些选择,如:
多项式核函数(Polynomial Kernel)
字符串核函数(String kernel)
卡方核函数( chi-square kernel)
直方图交集核函数(histogram intersection kernel)
等等…
这些核函数的目标也都是根据训练集和地标之间的距离来构建新特征,这些核函数需要满足Mercer’s定理,才能被支持向量机的优化软件正确处理。
多类分类问题
假设我们利用之前介绍的一对多方法来解决一个多类分类问题。如果一共有 k k k个类,则我们需要 k k k个模型,以及 k k k个参数向量 θ { {\theta }} θ。我们同样也可以训练 k k k个支持向量机来解决多类分类问题。但是大多数支持向量机软件包都有内置的多类分类功能,我们只要直接使用即可。
尽管你不去写你自己的SVM的优化软件,但是你也需要做几件事:
1、是提出参数 C C C的选择。我们在之前的视频中讨论过误差/方差在这方面的性质。
2、你也需要选择内核参数或你想要使用的相似函数,其中一个选择是:我们选择不需要任何内核参数,没有内核参数的理念,也叫线性核函数。因此,如果有人说他使用了线性核的SVM(支持向量机),这就意味这他使用了不带有核函数的SVM(支持向量机)。
从逻辑回归模型,我们得到了支持向量机模型,在两者之间,我们应该如何选择呢?
下面是一些普遍使用的准则:
n n n为特征数, m m m为训练样本数。
(1)如果相较于 m m m而言, n n n要大许多,即训练集数据量不够支持我们训练一个复杂的非线性模型,我们选用逻辑回归模型或者不带核函数的支持向量机。
(2)如果 n n n较小,而且 m m m大小中等,例如 n n n在 1-1000 之间,而 m m m在10-10000之间,使用高斯核函数的支持向量机。
(3)如果 n n n较小,而 m m m较大,例如 n n n在1-1000之间,而 m m m大于50000,则使用支持向量机会非常慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的支持向量机。
值得一提的是,神经网络在以上三种情况下都可能会有较好的表现,但是训练神经网络可能非常慢,选择支持向量机的原因主要在于它的代价函数是凸函数,不存在局部最小值。
聚类(Clustering)
13.1 无监督学习:简介
在一个典型的监督学习中,我们有一个有标签的训练集,我们的目标是找到能够区分正样本和负样本的决策边界,在这里的监督学习中,我们有一系列标签,我们需要据此拟合一个假设函数。与此不同的是,在非监督学习中,我们的数据没有附带任何标签
13.2 K-均值算法
K-均值是最普及的聚类算法,算法接受一个未标记的数据集,然后将数据聚类成不同的组。
K-均值是一个迭代算法,假设我们想要将数据聚类成n个组,其方法为:
首先选择 K K K个随机的点,称为聚类中心(cluster centroids);
对于数据集中的每一个数据,按照距离 K K K个中心点的距离,将其与距离最近的中心点关联起来,与同一个中心点关联的所有点聚成一类。
计算每一个组的平均值,将该组所关联的中心点移动到平均值的位置。
重复步骤2-4直至中心点不再变化。
13.3 优化目标
K-均值最小化问题,是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和,因此
K-均值的代价函数(又称畸变函数 Distortion function)为:
J ( c ( 1 ) , . . . , c ( m ) , μ 1 , . . . , μ K ) = 1 m ∑ i = 1 m ∥ X ( i ) − μ c ( i ) ∥ 2 J(c^{(1)},...,c^{(m)},μ_1,...,μ_K)=\dfrac {1}{m}\sum^{m}_{i=1}\left\| X^{\left( i\right) }-\mu_{c^{(i)}}\right\| ^{2} J(c(1),...,c(m),μ1,...,μK)=m1i=1∑m∥∥∥X(i)−μc(i)∥∥∥2
其中 μ c ( i ) {
{\mu }_{
{
{c}^{(i)}}}} μc(i)代表与 x ( i ) {
{x}^{(i)}} x(i)最近的聚类中心点。
我们的的优化目标便是找出使得代价函数最小的 c ( 1 ) c^{(1)} c(1), c ( 2 ) c^{(2)} c(2),…, c ( m ) c^{(m)} c(m)和 μ 1 μ^1 μ1, μ 2 μ^2 μ2,…, μ k μ^k μk:
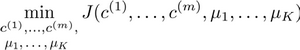
回顾刚才给出的:
K-均值迭代算法,我们知道,第一个循环是用于减小 c ( i ) c^{(i)} c(i)引起的代价,而第二个循环则是用于减小 μ i {
{\mu }_{i}} μi引起的代价。迭代的过程一定会是每一次迭代都在减小代价函数,不然便是出现了错误。
13.4 随机初始化
在运行K-均值算法的之前,我们首先要随机初始化所有的聚类中心点,下面介绍怎样做:
- 我们应该选择 K < m K<m K<m,即聚类中心点的个数要小于所有训练集实例的数量
- 随机选择 K K K个训练实例,然后令 K K K个聚类中心分别与这 K K K个训练实例相等
K-均值的一个问题在于,它有可能会停留在一个局部最小值处,而这取决于初始化的情况。
为了解决这个问题,我们通常需要多次运行K-均值算法,每一次都重新进行随机初始化,最后再比较多次运行K-均值的结果,选择代价函数最小的结果。这种方法在 K K K较小的时候(2–10)还是可行的,但是如果 K K K较大,这么做也可能不会有明显地改善。
13.5 选择聚类数
没有所谓最好的选择聚类数的方法,通常是需要根据不同的问题,人工进行选择的。选择的时候思考我们运用K-均值算法聚类的动机是什么,然后选择能最好服务于该目的标聚类数。
关于“肘部法则”,我们所需要做的是改变 K K K值,也就是聚类类别数目的总数。
聚类参考资料:
1.相似度/距离计算方法总结
(1). 闵可夫斯基距离Minkowski/(其中欧式距离: p = 2 p=2 p=2)
d i s t ( X , Y ) = ( ∑ i = 1 n ∣ x i − y i ∣ p ) 1 p dist(X,Y)={ {\left( { {\sum\limits_{i=1}^{n}{\left| { {x}_{i}}-{ {y}_{i}} \right|}}^{p}} \right)}^{\frac{1}{p}}} dist(X,Y)=(i=1∑n∣xi−yi∣p)p1
(2). 杰卡德相似系数(Jaccard):
J ( A , B ) = ∣ A ∩ B ∣ ∣ A ∪ B ∣ J(A,B)=\frac{\left| A\cap B \right|}{\left|A\cup B \right|} J(A,B)=∣A∪B∣∣A∩B∣
(3). 余弦相似度(cosine similarity):
n n n维向量 x x x和 y y y的夹角记做 θ \theta θ,根据余弦定理,其余弦值为:
c o s ( θ ) = x T y ∣ x ∣ ⋅ ∣ y ∣ = ∑ i = 1 n x i y i ∑ i = 1 n x i 2 ∑ i = 1 n y i 2 cos (\theta )=\frac{
{
{x}^{T}}y}{\left|x \right|\cdot \left| y \right|}=\frac{\sum\limits_{i=1}^{n}{
{
{x}_{i}}{
{y}_{i}}}}{\sqrt{\sum\limits_{i=1}^{n}{
{
{x}_{i}}^{2}}}\sqrt{\sum\limits_{i=1}^{n}{
{
{y}_{i}}^{2}}}} cos(θ)=∣x∣⋅∣y∣xTy=i=1∑nxi2i=1∑nyi2i=1∑nxiyi
(4). Pearson皮尔逊相关系数:
ρ X Y = cov ( X , Y ) σ X σ Y = E [ ( X − μ X ) ( Y − μ Y ) ] σ X σ Y = ∑ i = 1 n ( x − μ X ) ( y − μ Y ) ∑ i = 1 n ( x − μ X ) 2 ∑ i = 1 n ( y − μ Y ) 2 {
{\rho }_{XY}}=\frac{\operatorname{cov}(X,Y)}{
{
{\sigma }_{X}}{
{\sigma }_{Y}}}=\frac{E[(X-{
{\mu }_{X}})(Y-{
{\mu }_{Y}})]}{
{
{\sigma }_{X}}{
{\sigma }_{Y}}}=\frac{\sum\limits_{i=1}^{n}{(x-{
{\mu }_{X}})(y-{
{\mu }_{Y}})}}{\sqrt{\sum\limits_{i=1}^{n}{
{
{(x-{
{\mu }_{X}})}^{2}}}}\sqrt{\sum\limits_{i=1}^{n}{
{
{(y-{
{\mu }_{Y}})}^{2}}}}} ρXY=σXσYcov(X,Y)=σXσYE[(X−μX)(Y−μY)]=i=1∑n(x−μX)2i=1∑n(y−μY)2i=1∑n(x−μX)(y−μY)
Pearson相关系数即将 x x x、 y y y坐标向量各自平移到原点后的夹角余弦。
2.聚类的衡量指标
(1). 均一性: p p p
类似于精确率,一个簇中只包含一个类别的样本,则满足均一性。其实也可以认为就是正确率(每个 聚簇中正确分类的样本数占该聚簇总样本数的比例和)
(2). 完整性: r r r
类似于召回率,同类别样本被归类到相同簇中,则满足完整性;每个聚簇中正确分类的样本数占该
类型的总样本数比例的和
(3). V-measure:
均一性和完整性的加权平均
V = ( 1 + β 2 ) ∗ p r β 2 ∗ p + r V = \frac{(1+\beta^2)*pr}{\beta^2*p+r} V=β2∗p+r(1+β2)∗pr
(4). 轮廓系数
样本 i i i的轮廓系数: s ( i ) s(i) s(i)
簇内不相似度:计算样本 i i i到同簇其它样本的平均距离为 a ( i ) a(i) a(i),应尽可能小。
簇间不相似度:计算样本 i i i到其它簇 C j C_j Cj的所有样本的平均距离 b i j b_{ij} bij,应尽可能大。
轮廓系数: s ( i ) s(i) s(i)值越接近1表示样本 i i i聚类越合理,越接近-1,表示样本 i i i应该分类到 另外的簇中,近似为0,表示样本 i i i应该在边界上;所有样本的 s ( i ) s(i) s(i)的均值被成为聚类结果的轮廓系数。
s ( i ) = b ( i ) − a ( i ) m a x { a ( i ) , b ( i ) } s(i) = \frac{b(i)-a(i)}{max\{a(i),b(i)\}} s(i)=max{ a(i),b(i)}b(i)−a(i)
(5). ARI
数据集 S S S共有 N N N个元素, 两个聚类结果分别是:
X = { X 1 , X 2 , . . . , X r } , Y = { Y 1 , Y 2 , . . . , Y s } X=\{ { {X}_{1}},{ {X}_{2}},...,{ {X}_{r}}\},Y=\{ { {Y}_{1}},{ {Y}_{2}},...,{ {Y}_{s}}\} X={ X1,X2,...,Xr},Y={ Y1,Y2,...,Ys}
X X X和 Y Y Y的元素个数为:
a = { a 1 , a 2 , . . . , a r } , b = { b 1 , b 2 , . . . , b s } a=\{ { {a}_{1}},{ {a}_{2}},...,{ {a}_{r}}\},b=\{ { {b}_{1}},{ {b}_{2}},...,{ {b}_{s}}\} a={ a1,a2,...,ar},b={ b1,b2,...,bs}
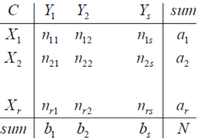
记: n i j = ∣ X i ∩ Y i ∣ { {n}_{ij}}=\left| { {X}_{i}}\cap { {Y}_{i}} \right| nij=∣Xi∩Yi∣
A R I = ∑ i , j C n i j 2 − [ ( ∑ i C a i 2 ) ⋅ ( ∑ i C b i 2 ) ] / C n 2 1 2 [ ( ∑ i C a i 2 ) + ( ∑ i C b i 2 ) ] − [ ( ∑ i C a i 2 ) ⋅ ( ∑ i C b i 2 ) ] / C n 2 ARI=\frac{\sum\limits_{i,j}{C_{ { {n}_{ij}}}^{2}}-\left[ \left( \sum\limits_{i}{C_{ { {a}_{i}}}^{2}} \right)\cdot \left( \sum\limits_{i}{C_{ { {b}_{i}}}^{2}} \right) \right]/C_{n}^{2}}{\frac{1}{2}\left[ \left( \sum\limits_{i}{C_{ { {a}_{i}}}^{2}} \right)+\left( \sum\limits_{i}{C_{ { {b}_{i}}}^{2}} \right) \right]-\left[ \left( \sum\limits_{i}{C_{ { {a}_{i}}}^{2}} \right)\cdot \left( \sum\limits_{i}{C_{ { {b}_{i}}}^{2}} \right) \right]/C_{n}^{2}} ARI=21[(i∑Cai2)+(i∑Cbi2)]−[(i∑Cai2)⋅(i∑Cbi2)]/Cn2i,j∑Cnij2−[(i∑Cai2)⋅(i∑Cbi2)]/Cn2
降维(Dimensionality Reduction)
14.1 动机一:数据压缩
第二种类型的无监督学习问题,称为降维。有几个不同的的原因使你可能想要做降维。一是数据压缩,后面我们会看了一些视频后,数据压缩不仅允许我们压缩数据,因而使用较少的计算机内存或磁盘空间,但它也让我们加快我们的学习算法。
14.2 动机二:数据可视化
在许多及其学习问题中,如果我们能将数据可视化,我们便能寻找到一个更好的解决方案,降维可以帮助我们。
这样做的问题在于,降维的算法只负责减少维数,新产生的特征的意义就必须由我们自己去发现了。
14.3 主成分分析问题
主成分分析(PCA)是最常见的降维算法。
在PCA中,我们要做的是找到一个方向向量(Vector direction),当我们把所有的数据都投射到该向量上时,我们希望投射平均均方误差能尽可能地小。方向向量是一个经过原点的向量,而投射误差是从特征向量向该方向向量作垂线的长度。
面给出主成分分析问题的描述:
问题是要将 n n n维数据降至 k k k维,目标是找到向量 u ( 1 ) u^{(1)} u(1), u ( 2 ) u^{(2)} u(2),…, u ( k ) u^{(k)} u(k)使得总的投射误差最小。主成分分析与线性回顾的比较:
主成分分析与线性回归是两种不同的算法。主成分分析最小化的是投射误差(Projected Error),而线性回归尝试的是最小化预测误差。线性回归的目的是预测结果,而主成分分析不作任何预测。
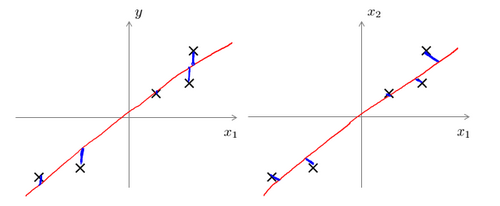
左边的是线性回归的误差(垂直于横轴投影),右边则是主要成分分析的误差(垂直于红线投影)。
PCA将 n n n个特征降维到 k k k个,可以用来进行数据压缩,如果100维的向量最后可以用10维来表示,那么压缩率为90%。同样图像处理领域的KL变换使用PCA做图像压缩。但PCA 要保证降维后,还要保证数据的特性损失最小。
PCA技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序,根据需要取前面最重要的部分,将后面的维数省去,可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
PCA技术的一个很大的优点是,它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。
但是,这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。
14.4 主成分分析算法
PCA 减少 n n n维到 k k k维:
第一步是均值归一化。我们需要计算出所有特征的均值,然后令 x j = x j − μ j x_j= x_j-μ_j xj=xj−μj。如果特征是在不同的数量级上,我们还需要将其除以标准差 σ 2 σ^2 σ2。
第二步是计算协方差矩阵(covariance matrix) Σ Σ Σ:
∑ = 1 m ∑ i = 1 n ( x ( i ) ) ( x ( i ) ) T \sum=\dfrac {1}{m}\sum^{n}_{i=1}\left( x^{(i)}\right) \left( x^{(i)}\right) ^{T} ∑=m1∑i=1n(x(i))(x(i))T
第三步是计算协方差矩阵 Σ Σ Σ的特征向量(eigenvectors):
在 Octave 里我们可以利用奇异值分解(singular value decomposition)来求解,[U, S, V]= svd(sigma)。
如果我们希望将数据从 n n n维降至 k k k维,我们只需要从 U U U中选取前 k k k个向量,获得一个 n × k n×k n×k维度的矩阵,我们用 U r e d u c e U_{reduce} Ureduce表示,然后通过如下计算获得要求的新特征向量 z ( i ) z^{(i)} z(i):
z ( i ) = U r e d u c e T ∗ x ( i ) z^{(i)}=U^{T}_{reduce}*x^{(i)} z(i)=UreduceT∗x(i)
其中 x x x是 n × 1 n×1 n×1维的,因此结果为 k × 1 k×1 k×1维度。注,我们不对方差特征进行处理。
14.5 选择主成分的数量
主要成分分析是减少投射的平均均方误差:
训练集的方差为: 1 m ∑ i = 1 m ∥ x ( i ) ∥ 2 \dfrac {1}{m}\sum^{m}_{i=1}\left\| x^{\left( i\right) }\right\| ^{2} m1∑i=1m∥∥x(i)∥∥2
我们希望在平均均方误差与训练集方差的比例尽可能小的情况下选择尽可能小的 k k k值。
我们可以先令 k = 1 k=1 k=1,然后进行主要成分分析,获得 U r e d u c e U_{reduce} Ureduce和 z z z,然后计算比例是否小于1%。如果不是的话再令 k = 2 k=2 k=2,如此类推,直到找到可以使得比例小于1%的最小 k k k 值(原因是各个特征之间通常情况存在某种相关性)。
还有一些更好的方式来选择 k k k,当我们在Octave中调用“svd”函数的时候,我们获得三个参数:[U, S, V] = svd(sigma)
其中的 S S S是一个 n × n n×n n×n的矩阵,只有对角线上有值,而其它单元都是0,我们可以使用这个矩阵来计算平均均方误差与训练集方差的比例:
方差越大,表明这个特征里数据分布的离散程度就越大,特征所包含的信息量就越大;反之,如果特征里数据的方差小,分布集中,则表明其包含的信息量就小。那么,我们自然选择保留信息量大的那个特征了。
1 m ∑ i = 1 m ∥ x ( i ) − x a p p r o x ( i ) ∥ 2 1 m ∑ i = 1 m ∥ x ( i ) ∥ 2 = 1 − Σ i = 1 k S i i Σ i = 1 m S i i ≤ 1 % \dfrac {\dfrac {1}{m}\sum^{m}_{i=1}\left\| x^{\left( i\right) }-x^{\left( i\right) }_{approx}\right\| ^{2}}{\dfrac {1}{m}\sum^{m}_{i=1}\left\| x^{(i)}\right\| ^{2}}=1-\dfrac {\Sigma^{k}_{i=1}S_{ii}}{\Sigma^{m}_{i=1}S_{ii}}\leq 1\% m1∑i=1m∥∥x(i)∥∥2m1∑i=1m∥∥∥x(i)−xapprox(i)∥∥∥2=1−Σi=1mSiiΣi=1kSii≤1%
也就是: Σ i = 1 k s i i Σ i = 1 n s i i ≥ 0.99 \frac {\Sigma^{k}_{i=1}s_{ii}}{\Sigma^{n}_{i=1}s_{ii}}\geq0.99 Σi=1nsiiΣi=1ksii≥0.99
在压缩过数据后,我们可以采用如下方法来近似地获得原有的特征: x a p p r o x ( i ) = U r e d u c e z ( i ) x^{\left( i\right) }_{approx}=U_{reduce}z^{(i)} xapprox(i)=Ureducez(i)
14.6 重建的压缩表示
PCA算法,我们可能有一个这样的样本。如图中样本 x ( 1 ) x^{(1)} x(1), x ( 2 ) x^{(2)} x(2)。我们做的是,我们把这些样本投射到图中这个一维平面。然后现在我们需要只使用一个实数,比如 z ( 1 ) z^{(1)} z(1),指定这些点的位置后他们被投射到这一个三维曲面。给定一个点 z ( 1 ) z^{(1)} z(1),我们怎么能回去这个原始的二维空间呢? x x x为2维, z z z为1维, z = U r e d u c e T x z=U^{T}_{reduce}x z=UreduceTx,相反的方程为: x a p p o x = U r e d u c e ⋅ z x_{appox}=U_{reduce}\cdot z xappox=Ureduce⋅z, x a p p o x ≈ x x_{appox}\approx x xappox≈x。
14.7 主成分分析法的应用建议
1. 第一步是运用主要成分分析将数据压缩至1000个特征
2. 然后对**训练集**运行学习算法
3. 在预测时,采用之前学习而来的$U_{reduce}$将输入的特征$x$转换成特征向量$z$,然后再进行预测
注:如果我们有交叉验证集合测试集,也采用对训练集学习而来的 U r e d u c e U_{reduce} Ureduce。
错误的主要成分分析情况:一个常见错误使用主要成分分析的情况是,将其用于减少过拟合(减少了特征的数量)。这样做非常不好,不如尝试正则化处理。原因在于主要成分分析只是近似地丢弃掉一些特征,它并不考虑任何与结果变量有关的信息,因此可能会丢失非常重要的特征。然而当我们进行正则化处理时,会考虑到结果变量,不会丢掉重要的数据。
另一个常见的错误是,默认地将主要成分分析作为学习过程中的一部分,这虽然很多时候有效果,最好还是从所有原始特征开始,只在有必要的时候(算法运行太慢或者占用太多内存)才考虑采用主要成分分析。
异常检测(Anomaly Detection)
15.1 问题的动机
异常检测(Anomaly detection)问题。这是机器学习算法的一个常见应用。这种算法的一个有趣之处在于:它虽然主要用于非监督学习问题,但从某些角度看,它又类似于一些监督学习问题。
给定数据集 x ( 1 ) , x ( 2 ) , . . , x ( m ) x^{(1)},x^{(2)},..,x^{(m)} x(1),x(2),..,x(m),我们假使数据集是正常的,我们希望知道新的数据 x t e s t x_{test} xtest 是不是异常的,即这个测试数据不属于该组数据的几率如何。我们所构建的模型应该能根据该测试数据的位置告诉我们其属于一组数据的可能性 p ( x ) p(x) p(x)。
上图中,在蓝色圈内的数据属于该组数据的可能性较高,而越是偏远的数据,其属于该组数据的可能性就越低。
这种方法称为密度估计,表达如下:
$$
if \quad p(x)
\begin{cases}
< \varepsilon & anomaly \
=\varepsilon & normal
\end{cases}
$$
欺诈检测:
x ( i ) = 用 户 的 第 i 个 活 动 特 征 x^{(i)} = {用户的第i个活动特征} x(i)=用户的第i个活动特征
模型 p ( x ) p(x) p(x) 为我们其属于一组数据的可能性,通过 p ( x ) < ε p(x) < \varepsilon p(x)<ε检测非正常用户。
异常检测主要用来识别欺骗。例如在线采集而来的有关用户的数据,一个特征向量中可能会包含如:用户多久登录一次,访问过的页面,在论坛发布的帖子数量,甚至是打字速度等。尝试根据这些特征构建一个模型,可以用这个模型来识别那些不符合该模式的用户。
15.2 高斯分布
回顾高斯分布的基本知识。
通常如果我们认为变量 x x x 符合高斯分布 x ∼ N ( μ , σ 2 ) x \sim N(\mu, \sigma^2) x∼N(μ,σ2)则其概率密度函数为:
p ( x , μ , σ 2 ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) p(x,\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) p(x,μ,σ2)=2πσ1exp(−2σ2(x−μ)2)
我们可以利用已有的数据来预测总体中的 μ μ μ和 σ 2 σ^2 σ2的计算方法如下:
μ = 1 m ∑ i = 1 m x ( i ) \mu=\frac{1}{m}\sum\limits_{i=1}^{m}x^{(i)} μ=m1i=1∑mx(i)
σ 2 = 1 m ∑ i = 1 m ( x ( i ) − μ ) 2 \sigma^2=\frac{1}{m}\sum\limits_{i=1}^{m}(x^{(i)}-\mu)^2 σ2=m1i=1∑m(x(i)−μ)2
注:机器学习中对于方差我们通常只除以 m m m而非统计学中的 ( m − 1 ) (m-1) (m−1)。这里顺便提一下,在实际使用中,到底是选择使用 1 / m 1/m 1/m还是 1 / ( m − 1 ) 1/(m-1) 1/(m−1)其实区别很小,只要你有一个还算大的训练集,在机器学习领域大部分人更习惯使用 1 / m 1/m 1/m这个版本的公式。这两个版本的公式在理论特性和数学特性上稍有不同,但是在实际使用中,他们的区别甚小,几乎可以忽略不计。
15.3 算法
异常检测算法:
对于给定的数据集 x ( 1 ) , x ( 2 ) , . . . , x ( m ) x^{(1)},x^{(2)},...,x^{(m)} x(1),x(2),...,x(m),我们要针对每一个特征计算 μ \mu μ 和 σ 2 \sigma^2 σ2 的估计值。
μ j = 1 m ∑ i = 1 m x j ( i ) \mu_j=\frac{1}{m}\sum\limits_{i=1}^{m}x_j^{(i)} μj=m1i=1∑mxj(i)
σ j 2 = 1 m ∑ i = 1 m ( x j ( i ) − μ j ) 2 \sigma_j^2=\frac{1}{m}\sum\limits_{i=1}^m(x_j^{(i)}-\mu_j)^2 σj2=m1i=1∑m(xj(i)−μj)2
一旦我们获得了平均值和方差的估计值,给定新的一个训练实例,根据模型计算 p ( x ) p(x) p(x):
p ( x ) = ∏ j = 1 n p ( x j ; μ j , σ j 2 ) = ∏ j = 1 1 1 2 π σ j e x p ( − ( x j − μ j ) 2 2 σ j 2 ) p(x)=\prod\limits_{j=1}^np(x_j;\mu_j,\sigma_j^2)=\prod\limits_{j=1}^1\frac{1}{\sqrt{2\pi}\sigma_j}exp(-\frac{(x_j-\mu_j)^2}{2\sigma_j^2}) p(x)=j=1∏np(xj;μj,σj2)=j=1∏12πσj1exp(−2σj2(xj−μj)2)
当 p ( x ) < ε p(x) < \varepsilon p(x)<ε时,为异常。
我们选择一个 ε \varepsilon ε,将 p ( x ) = ε p(x) = \varepsilon p(x)=ε作为我们的判定边界,当 p ( x ) > ε p(x) > \varepsilon p(x)>ε时预测数据为正常数据,否则为异常。
15.4 开发和评价一个异常检测系统
异常检测算法是一个非监督学习算法,意味着我们无法根据结果变量 $ y$ 的值来告诉我们数据是否真的是异常的。我们需要另一种方法来帮助检验算法是否有效。当我们开发一个异常检测系统时,我们从带标记(异常或正常)的数据着手,我们从其中选择一部分正常数据用于构建训练集,然后用剩下的正常数据和异常数据混合的数据构成交叉检验集和测试集。
具体的评价方法如下:
-
根据测试集数据,我们估计特征的平均值和方差并构建 p ( x ) p(x) p(x)函数
-
对交叉检验集,我们尝试使用不同的 ε \varepsilon ε值作为阀值,并预测数据是否异常,根据 F 1 F1 F1值或者查准率与查全率的比例来选择 ε \varepsilon ε
-
选出 ε \varepsilon ε 后,针对测试集进行预测,计算异常检验系统的 F 1 F1 F1值,或者查准率与查全率之比
15.5 异常检测与监督学习对比
| 异常检测 | 监督学习 |
|---|---|
| 非常少量的正向类(异常数据 y = 1 y=1 y=1), 大量的负向类( y = 0 y=0 y=0) | 同时有大量的正向类和负向类 |
| 许多不同种类的异常,非常难。根据非常 少量的正向类数据来训练算法。 | 有足够多的正向类实例,足够用于训练 算法,未来遇到的正向类实例可能与训练集中的非常近似。 |
| 未来遇到的异常可能与已掌握的异常、非常的不同。 | |
| 例如: 欺诈行为检测 生产(例如飞机引擎)检测数据中心的计算机运行状况 | 例如:邮件过滤器 天气预报 肿瘤分类 |
15.6 选择特征
对于异常检测算法,我们使用的特征是至关重要的,下面谈谈如何选择特征:
异常检测假设特征符合高斯分布,如果数据的分布不是高斯分布,异常检测算法也能够工作,但是最好还是将数据转换成高斯分布
误差分析:
一个常见的问题是一些异常的数据可能也会有较高的 p ( x ) p(x) p(x)值,因而被算法认为是正常的。这种情况下误差分析能够帮助我们,我们可以分析那些被算法错误预测为正常的数据,观察能否找出一些问题。我们可能能从问题中发现我们需要增加一些新的特征,增加这些新特征后获得的新算法能够帮助我们更好地进行异常检测。
我们通常可以通过将一些相关的特征进行组合,来获得一些新的更好的特征(异常数据的该特征值异常地大或小),例如,在检测数据中心的计算机状况的例子中,我们可以用CPU负载与网络通信量的比例作为一个新的特征,如果该值异常地大,便有可能意味着该服务器是陷入了一些问题中。
15.7 多元高斯分布(选修)
假使我们有两个相关的特征,而且这两个特征的值域范围比较宽,这种情况下,一般的高斯分布模型可能不能很好地识别异常数据。其原因在于,一般的高斯分布模型尝试的是去同时抓住两个特征的偏差,因此创造出一个比较大的判定边界。
下图中是两个相关特征,洋红色的线(根据ε的不同其范围可大可小)是一般的高斯分布模型获得的判定边界,很明显绿色的X所代表的数据点很可能是异常值,但是其 p ( x ) p(x) p(x)值却仍然在正常范围内。多元高斯分布将创建像图中蓝色曲线所示的判定边界。
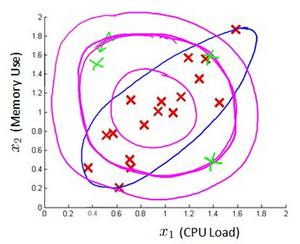
在一般的高斯分布模型中,我们计算 p ( x ) p(x) p(x) 的方法是:
通过分别计算每个特征对应的几率然后将其累乘起来,在多元高斯分布模型中,我们将构建特征的协方差矩阵,用所有的特征一起来计算 p ( x ) p(x) p(x)。
我们首先计算所有特征的平均值,然后再计算协方差矩阵:
p ( x ) = ∏ j = 1 n p ( x j ; μ , σ j 2 ) = ∏ j = 1 n 1 2 π σ j e x p ( − ( x j − μ j ) 2 2 σ j 2 ) p(x)=\prod_{j=1}^np(x_j;\mu,\sigma_j^2)=\prod_{j=1}^n\frac{1}{\sqrt{2\pi}\sigma_j}exp(-\frac{(x_j-\mu_j)^2}{2\sigma_j^2}) p(x)=∏j=1np(xj;μ,σj2)=∏j=1n2πσj1exp(−2σj2(xj−μj)2)
μ = 1 m ∑ i = 1 m x ( i ) \mu=\frac{1}{m}\sum_{i=1}^mx^{(i)} μ=m1∑i=1mx(i)
Σ = 1 m ∑ i = 1 m ( x ( i ) − μ ) ( x ( i ) − μ ) T = 1 m ( X − μ ) T ( X − μ ) \Sigma = \frac{1}{m}\sum_{i=1}^m(x^{(i)}-\mu)(x^{(i)}-\mu)^T=\frac{1}{m}(X-\mu)^T(X-\mu) Σ=m1∑i=1m(x(i)−μ)(x(i)−μ)T=m1(X−μ)T(X−μ)
注:其中$\mu $ 是一个向量,其每一个单元都是原特征矩阵中一行数据的均值。最后我们计算多元高斯分布的 p ( x ) p\left( x \right) p(x):
p ( x ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) p(x)=\frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right) p(x)=(2π)2n∣Σ∣211exp(−21(x−μ)TΣ−1(x−μ))
其中:
∣ Σ ∣ |\Sigma| ∣Σ∣是定矩阵,在 Octave 中用 det(sigma)计算
Σ − 1 \Sigma^{-1} Σ−1 是逆矩阵,下面我们来看看协方差矩阵是如何影响模型的:
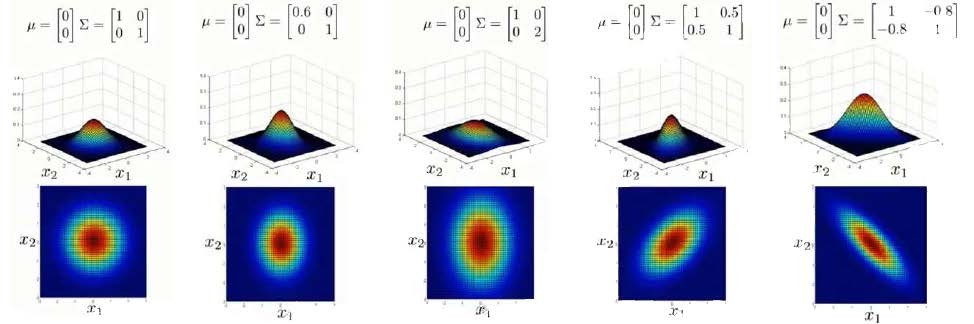
上图是5个不同的模型,从左往右依次分析:
-
是一个一般的高斯分布模型
-
通过协方差矩阵,令特征1拥有较小的偏差,同时保持特征2的偏差
-
通过协方差矩阵,令特征2拥有较大的偏差,同时保持特征1的偏差
-
通过协方差矩阵,在不改变两个特征的原有偏差的基础上,增加两者之间的正相关性
-
通过协方差矩阵,在不改变两个特征的原有偏差的基础上,增加两者之间的负相关性
多元高斯分布模型与原高斯分布模型的关系:
可以证明的是,原本的高斯分布模型是多元高斯分布模型的一个子集,即像上图中的第1、2、3,3个例子所示,如果协方差矩阵只在对角线的单位上有非零的值时,即为原本的高斯分布模型了。
原高斯分布模型和多元高斯分布模型的比较:
| 原高斯分布模型 | 多元高斯分布模型 |
|---|---|
| 不能捕捉特征之间的相关性 但可以通过将特征进行组合的方法来解决 | 自动捕捉特征之间的相关性 |
| 计算代价低,能适应大规模的特征 | 计算代价较高 训练集较小时也同样适用 |
| 必须要有 m > n m>n m>n,不然的话协方差矩阵 Σ \Sigma Σ不可逆的,通常需要 m > 10 n m>10n m>10n 另外特征冗余也会导致协方差矩阵不可逆 |
原高斯分布模型被广泛使用着,如果特征之间在某种程度上存在相互关联的情况,我们可以通过构造新新特征的方法来捕捉这些相关性。
如果训练集不是太大,并且没有太多的特征,我们可以使用多元高斯分布模型。
15.8 使用多元高斯分布进行异常检测(可选)
原始模型和多元高斯分布比较如图:

推荐系统(Recommender Systems)
16.1 问题形式化
机器学习中的大思想
我们从一个例子开始定义推荐系统的问题。
假使我们是一个电影供应商,我们有 5 部电影和 4 个用户,我们要求用户为电影打分。
16.2 基于内容的推荐系统
针对用户 j j j,该线性回归模型的代价为预测误差的平方和,加上正则化项:
min θ ( j ) 1 2 ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ( θ k ( j ) ) 2 \min_{\theta (j)}\frac{1}{2}\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2+\frac{\lambda}{2}\left(\theta_{k}^{(j)}\right)^2 θ(j)min21i:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λ(θk(j))2
其中 i : r ( i , j ) i:r(i,j) i:r(i,j)表示我们只计算那些用户 j j j 评过分的电影。在一般的线性回归模型中,误差项和正则项应该都是乘以 1 / 2 m 1/2m 1/2m,在这里我们将 m m m去掉。并且我们不对方差项 θ 0 \theta_0 θ0进行正则化处理。
上面的代价函数只是针对一个用户的,为了学习所有用户,我们将所有用户的代价函数求和:
min θ ( 1 ) , . . . , θ ( n u ) 1 2 ∑ j = 1 n u ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2 \min_{\theta^{(1)},...,\theta^{(n_u)}} \frac{1}{2}\sum_{j=1}^{n_u}\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2 θ(1),...,θ(nu)min21j=1∑nui:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λj=1∑nuk=1∑n(θk(j))2
如果我们要用梯度下降法来求解最优解,我们计算代价函数的偏导数后得到梯度下降的更新公式为:
θ k ( j ) : = θ k ( j ) − α ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) x k ( i ) ( for k = 0 ) \theta_k^{(j)}:=\theta_k^{(j)}-\alpha\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x_{k}^{(i)} \quad (\text{for} \, k = 0) θk(j):=θk(j)−αi:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))xk(i)(fork=0)
θ k ( j ) : = θ k ( j ) − α ( ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) x k ( i ) + λ θ k ( j ) ) ( for k ≠ 0 ) \theta_k^{(j)}:=\theta_k^{(j)}-\alpha\left(\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x_{k}^{(i)}+\lambda\theta_k^{(j)}\right) \quad (\text{for} \, k\neq 0) θk(j):=θk(j)−α⎝⎛i:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))xk(i)+λθk(j)⎠⎞(fork=0)
16.3 协同过滤
相反地,如果我们拥有用户的参数,我们可以学习得出电影的特征。
m i n x ( 1 ) , . . . , x ( n m ) 1 2 ∑ i = 1 n m ∑ j r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ i = 1 n m ∑ k = 1 n ( x k ( i ) ) 2 \mathop{min}\limits_{x^{(1)},...,x^{(n_m)}}\frac{1}{2}\sum_{i=1}^{n_m}\sum_{j{r(i,j)=1}}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_k^{(i)})^2 x(1),...,x(nm)min21i=1∑nmjr(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λi=1∑nmk=1∑n(xk(i))2
但是如果我们既没有用户的参数,也没有电影的特征,这两种方法都不可行了。协同过滤算法可以同时学习这两者。
我们的优化目标便改为同时针对 x x x和 θ \theta θ进行。
J ( x ( 1 ) , . . . x ( n m ) , θ ( 1 ) , . . . , θ ( n u ) ) = 1 2 ∑ ( i : j ) : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ i = 1 n m ∑ k = 1 n ( x k ( j ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2 J(x^{(1)},...x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)})=\frac{1}{2}\sum_{(i:j):r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_k^{(j)})^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2 J(x(1),...x(nm),θ(1),...,θ(nu))=21(i:j):r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λi=1∑nmk=1∑n(xk(j))2+2λj=1∑nuk=1∑n(θk(j))2
对代价函数求偏导数的结果如下:
x k ( i ) : = x k ( i ) − α ( ∑ j : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) θ k j + λ x k ( i ) ) x_k^{(i)}:=x_k^{(i)}-\alpha\left(\sum_{j:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\theta_k^{j}+\lambda x_k^{(i)}\right) xk(i):=xk(i)−α⎝⎛j:r(i,j)=1∑((θ(j))Tx(i)−y(i,j)θkj+λxk(i)⎠⎞
θ k ( i ) : = θ k ( i ) − α ( ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) x k ( i ) + λ θ k ( j ) ) \theta_k^{(i)}:=\theta_k^{(i)}-\alpha\left(\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}x_k^{(i)}+\lambda \theta_k^{(j)}\right) θk(i):=θk(i)−α⎝⎛i:r(i,j)=1∑((θ(j))Tx(i)−y(i,j)xk(i)+λθk(j)⎠⎞
注:在协同过滤从算法中,我们通常不使用方差项,如果需要的话,算法会自动学得。
协同过滤算法使用步骤如下:
-
初始 x ( 1 ) , x ( 1 ) , . . . x ( n m ) , θ ( 1 ) , θ ( 2 ) , . . . , θ ( n u ) x^{(1)},x^{(1)},...x^{(nm)},\ \theta^{(1)},\theta^{(2)},...,\theta^{(n_u)} x(1),x(1),...x(nm), θ(1),θ(2),...,θ(nu)为一些随机小值
-
使用梯度下降算法最小化代价函数
-
在训练完算法后,我们预测 ( θ ( j ) ) T x ( i ) (\theta^{(j)})^Tx^{(i)} (θ(j))Tx(i)为用户 j j j 给电影 i i i 的评分
16.4 协同过滤算法
协同过滤优化目标:
给定 x ( 1 ) , . . . , x ( n m ) x^{(1)},...,x^{(n_m)} x(1),...,x(nm),估计 θ ( 1 ) , . . . , θ ( n u ) \theta^{(1)},...,\theta^{(n_u)} θ(1),...,θ(nu):
min θ ( 1 ) , . . . , θ ( n u ) 1 2 ∑ j = 1 n u ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2 \min_{\theta^{(1)},...,\theta^{(n_u)}}\frac{1}{2}\sum_{j=1}^{n_u}\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2 θ(1),...,θ(nu)min21j=1∑nui:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λj=1∑nuk=1∑n(θk(j))2
给定 θ ( 1 ) , . . . , θ ( n u ) \theta^{(1)},...,\theta^{(n_u)} θ(1),...,θ(nu),估计 x ( 1 ) , . . . , x ( n m ) x^{(1)},...,x^{(n_m)} x(1),...,x(nm):
同时最小化 x ( 1 ) , . . . , x ( n m ) x^{(1)},...,x^{(n_m)} x(1),...,x(nm)和 θ ( 1 ) , . . . , θ ( n u ) \theta^{(1)},...,\theta^{(n_u)} θ(1),...,θ(nu):
J ( x ( 1 ) , . . . , x ( n m ) , θ ( 1 ) , . . . , θ ( n u ) ) = 1 2 ∑ ( i , j ) : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ i = 1 n m ∑ k = 1 n ( x k ( i ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2 J(x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)})=\frac{1}{2}\sum_{(i,j):r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_k^{(i)})^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2 J(x(1),...,x(nm),θ(1),...,θ(nu))=21(i,j):r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λi=1∑nmk=1∑n(xk(i))2+2λj=1∑nuk=1∑n(θk(j))2
min x ( 1 ) , . . . , x ( n m ) θ ( 1 ) , . . . , θ ( n u ) J ( x ( 1 ) , . . . , x ( n m ) , θ ( 1 ) , . . . , θ ( n u ) ) \min_{x^{(1)},...,x^{(n_m)} \\\ \theta^{(1)},...,\theta^{(n_u)}}J(x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)}) x(1),...,x(nm) θ(1),...,θ(nu)minJ(x(1),...,x(nm),θ(1),...,θ(nu))
16.5 向量化:低秩矩阵分解
实现一种选择的方法,写出协同过滤算法的预测情况。
现在既然你已经对特征参数向量进行了学习,那么我们就会有一个很方便的方法来度量两部电影之间的相似性。例如说:电影 i i i 有一个特征向量 x ( i ) x^{(i)} x(i),你是否能找到一部不同的电影 j j j,保证两部电影的特征向量之间的距离 x ( i ) x^{(i)} x(i)和 x ( j ) x^{(j)} x(j)很小,那就能很有力地表明电影 i i i和电影 j j j 在某种程度上有相似,至少在某种意义上,某些人喜欢电影 i i i,或许更有可能也对电影 j j j 感兴趣。总结一下,当用户在看某部电影 i i i 的时候,如果你想找5部与电影非常相似的电影,为了能给用户推荐5部新电影,你需要做的是找出电影 j j j,在这些不同的电影中与我们要找的电影 i i i 的距离最小,这样你就能给你的用户推荐几部不同的电影了。
通过这个方法,希望你能知道,如何进行一个向量化的计算来对所有的用户和所有的电影进行评分计算。同时希望你也能掌握,通过学习特征参数,来找到相关电影和产品的方法。
16.6 推行工作上的细节:均值归一化
如果我们新增一个用户 Eve,并且 Eve 没有为任何电影评分,那么我们以什么为依据为Eve推荐电影呢?
我们首先需要对结果 $Y $矩阵进行均值归一化处理,将每一个用户对某一部电影的评分减去所有用户对该电影评分的平均值:
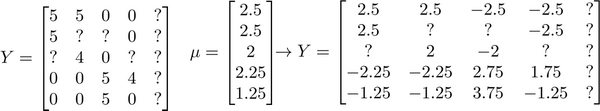
然后我们利用这个新的 Y Y Y 矩阵来训练算法。
如果我们要用新训练出的算法来预测评分,则需要将平均值重新加回去,预测 ( θ ( j ) ) T x ( i ) + μ i (\theta^{(j)})^T x^{(i)}+\mu_i (θ(j))Tx(i)+μi,对于Eve,我们的新模型会认为她给每部电影的评分都是该电影的平均分。
大规模机器学习(Large Scale Machine Learning)
17.1 大型数据集的学习
如果我们有一个低方差的模型,增加数据集的规模可以帮助你获得更好的结果。我们应该怎样应对一个有100万条记录的训练集?
首先应该做的事是去检查一个这么大规模的训练集是否真的必要,也许我们只用1000个训练集也能获得较好的效果,我们可以绘制学习曲线来帮助判断。
17.2 随机梯度下降法
如果我们一定需要一个大规模的训练集,我们可以尝试使用随机梯度下降法来代替批量梯度下降法。
在随机梯度下降法中,我们定义代价函数为一个单一训练实例的代价: c o s t ( θ , ( x ( i ) , y ( i ) ) ) = 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 cost\left( \theta, \left( {x}^{(i)} , {y}^{(i)} \right) \right) = \frac{1}{2}\left( {h}_{\theta}\left({x}^{(i)}\right)-{y}^{ {(i)}} \right)^{2} cost(θ,(x(i),y(i)))=21(hθ(x(i))−y(i))2
随机梯度下降算法为:首先对训练集随机“洗牌”,然后:
Repeat (usually anywhere between1-10){
for i = 1 : m i = 1:m i=1:m{
θ : = θ j − α ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta:={\theta}_{j}-\alpha\left( {h}_{\theta}\left({x}^{(i)}\right)-{y}^{(i)} \right){ {x}_{j}}^{(i)} θ:=θj−α(hθ(x(i))−y(i))xj(i)
(for j = 0 : n j=0:n j=0:n)
}
}
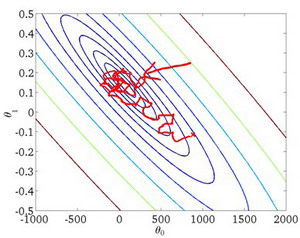
随机梯度下降算法在每一次计算之后便更新参数 θ { {\theta }} θ ,而不需要首先将所有的训练集求和,在梯度下降算法还没有完成一次迭代时,随机梯度下降算法便已经走出了很远。但是这样的算法存在的问题是,不是每一步都是朝着”正确”的方向迈出的。因此算法虽然会逐渐走向全局最小值的位置,但是可能无法站到那个最小值的那一点,而是在最小值点附近徘徊。
17.3 小批量梯度下降
小批量梯度下降算法是介于批量梯度下降算法和随机梯度下降算法之间的算法,每计算常数 b b b次训练实例,便更新一次参数 θ {
{\theta }} θ 。
Repeat {
for i = 1 : m i = 1:m i=1:m{
KaTeX parse error: Expected group after '_' at position 43: …\frac{1}{b}\sum_̲\limits{k=i}^{i…
(for j = 0 : n j=0:n j=0:n)
$ i +=10 $
}
}
通常我们会令 b b b 在 2-100 之间。这样做的好处在于,我们可以用向量化的方式来循环 b b b个训练实例,如果我们用的线性代数函数库比较好,能够支持平行处理,那么算法的总体表现将不受影响(与随机梯度下降相同)。
17.4 随机梯度下降收敛
在随机梯度下降中,我们在每一次更新 θ { {\theta }} θ 之前都计算一次代价,然后每 x x x次迭代后,求出这 x x x次对训练实例计算代价的平均值,然后绘制这些平均值与 x x x次迭代的次数之间的函数图表。

当我们绘制这样的图表时,可能会得到一个颠簸不平但是不会明显减少的函数图像(如上面左下图中蓝线所示)。我们可以增加 α α α来使得函数更加平缓,也许便能看出下降的趋势了(如上面左下图中红线所示);或者可能函数图表仍然是颠簸不平且不下降的(如洋红色线所示),那么我们的模型本身可能存在一些错误。
如果我们得到的曲线如上面右下方所示,不断地上升,那么我们可能会需要选择一个较小的学习率 α α α。
我们也可以令学习率随着迭代次数的增加而减小,例如令:
α = c o n s t 1 i t e r a t i o n N u m b e r + c o n s t 2 \alpha = \frac{const1}{iterationNumber + const2} α=iterationNumber+const2const1
随着我们不断地靠近全局最小值,通过减小学习率,我们迫使算法收敛而非在最小值附近徘徊。
但是通常我们不需要这样做便能有非常好的效果了,对 α α α进行调整所耗费的计算通常不值得
总结下,这段视频中,我们介绍了一种方法,近似地监测出随机梯度下降算法在最优化代价函数中的表现,这种方法不需要定时地扫描整个训练集,来算出整个样本集的代价函数,而是只需要每次对最后1000个,或者多少个样本,求一下平均值。应用这种方法,你既可以保证随机梯度下降法正在正常运转和收敛,也可以用它来调整学习速率 α α α的大小。
17.5 在线学习
在这个视频中,讨论一种新的大规模的机器学习机制,叫做在线学习机制。在线学习机制让我们可以模型化问题。
今天,许多大型网站或者许多大型网络公司,使用不同版本的在线学习机制算法,从大批的涌入又离开网站的用户身上进行学习。特别要提及的是,如果你有一个由连续的用户流引发的连续的数据流,进入你的网站,你能做的是使用一个在线学习机制,从数据流中学习用户的偏好,然后使用这些信息来优化一些关于网站的决策。
一个算法来从中学习的时候来模型化问题在线学习算法指的是对数据流而非离线的静态数据集的学习。许多在线网站都有持续不断的用户流,对于每一个用户,网站希望能在不将数据存储到数据库中便顺利地进行算法学习。
在线学习的算法与随机梯度下降算法有些类似,我们对单一的实例进行学习,而非对一个提前定义的训练集进行循环。
一旦对一个数据的学习完成了,我们便可以丢弃该数据,不需要再存储它了。这种方式的好处在于,我们的算法可以很好的适应用户的倾向性,算法可以针对用户的当前行为不断地更新模型以适应该用户。
每次交互事件并不只产生一个数据集,例如,我们一次给用户提供3个物流选项,用户选择2项,我们实际上可以获得3个新的训练实例,因而我们的算法可以一次从3个实例中学习并更新模型。
在线学习的一个优点就是,如果你有一个变化的用户群,又或者你在尝试预测的事情,在缓慢变化,就像你的用户的品味在缓慢变化,这个在线学习算法,可以慢慢地调试你所学习到的假设,将其调节更新到最新的用户行为。
17.6 映射化简和数据并行
映射化简和数据并行对于大规模机器学习问题而言是非常重要的概念。
如果我们能够将我们的数据集分配给不多台计算机,让每一台计算机处理数据集的一个子集,然后我们将计所的结果汇总在求和。这样的方法叫做映射简化。
具体而言,如果任何学习算法能够表达为,对训练集的函数的求和,那么便能将这个任务分配给多台计算机(或者同一台计算机的不同CPU 核心),以达到加速处理的目的。
应用实例:图片文字识别(Application Example: Photo OCR)
18.1 问题描述和流程图Problem Description and Pipeline
图像文字识别应用所作的事是,从一张给定的图片中识别文字。这比从一份扫描文档中识别文字要复杂的多。
为了完成这样的工作,需要采取如下步骤:
-
文字侦测(Text detection)——将图片上的文字与其他环境对象分离开来
-
字符切分(Character segmentation)——将文字分割成一个个单一的字符
-
字符分类(Character classification)——确定每一个字符是什么
可以用任务流程图来表达这个问题,每一项任务可以由一个单独的小队来负责解决:

18.2 滑动窗口
滑动窗口是一项用来从图像中抽取对象的技术。假使我们需要在一张图片中识别行人,首先要做的是用许多固定尺寸的图片来训练一个能够准确识别行人的模型。然后我们用之前训练识别行人的模型时所采用的图片尺寸在我们要进行行人识别的图片上进行剪裁,然后将剪裁得到的切片交给模型,让模型判断是否为行人,然后在图片上滑动剪裁区域重新进行剪裁,将新剪裁的切片也交给模型进行判断,如此循环直至将图片全部检测完。
滑动窗口技术也被用于文字识别,首先训练模型能够区分字符与非字符,然后,运用滑动窗口技术识别字符,一旦完成了字符的识别,我们将识别得出的区域进行一些扩展,然后将重叠的区域进行合并。接着我们以宽高比作为过滤条件,过滤掉高度比宽度更大的区域(认为单词的长度通常比高度要大)。
模型训练完后,我们仍然是使用滑动窗口技术来进行字符识别。
以上便是字符切分阶段。
最后一个阶段是字符分类阶段,利用神经网络、支持向量机或者逻辑回归算法训练一个分类器即可。
18.3 获取大量数据和人工数据
如果我们的模型是低方差的,那么获得更多的数据用于训练模型,是能够有更好的效果的。问题在于,我们怎样获得数据,数据不总是可以直接获得的,我们有可能需要人工地创造一些数据。
有关获得更多数据的几种方法:
1. 人工数据合成
2. 手动收集、标记数据
3. 众包
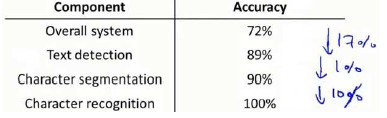
18.4 上限分析:哪部分管道的接下去做
在机器学习的应用中,我们通常需要通过几个步骤才能进行最终的预测,我们如何能够知道哪一部分最值得我们花时间和精力去改善呢?这个问题可以通过上限分析来回答。
总结(Conclusion)
作为这门课的结束时间,那么我们学到了些什么呢?在这门课中,我们花了大量的时间介绍了诸如线性回归、逻辑回归、神经网络、支持向量机等等一些监督学习算法,这类算法具有带标签的数据和样本,比如 x ( i ) { {x}^{\left( i \right)}} x(i)、 y ( i ) { {y}^{\left( i \right)}} y(i)。
然后我们也花了很多时间介绍无监督学习。例如 K-均值聚类、用于降维的主成分分析,以及当你只有一系列无标签数据 x ( i ) { {x}^{\left( i \right)}} x(i) 时的异常检测算法。
当然,有时带标签的数据,也可以用于异常检测算法的评估。此外,我们也花时间讨论了一些特别的应用或者特别的话题,比如说推荐系统。以及大规模机器学习系统,包括并行系统和映射化简方法,还有其他一些特别的应用。比如,用于计算机视觉技术的滑动窗口分类算法。
最后,我们还提到了很多关于构建机器学习系统的实用建议。这包括了怎样理解某个机器学习算法是否正常工作的原因,所以我们谈到了偏差和方差的问题,也谈到了解决方差问题的正则化,同时我们也讨论了怎样决定接下来怎么做的问题,也就是说当你在开发一个机器学习系统时,什么工作才是接下来应该优先考虑的问题。因此我们讨论了学习算法的评价法。介绍了评价矩阵,比如:查准率、召回率以及F1分数,还有评价学习算法比较实用的训练集、交叉验证集和测试集。我们也介绍了学习算法的调试,以及如何确保学习算法的正常运行,于是我们介绍了一些诊断法,比如学习曲线,同时也讨论了误差分析、上限分析等等内容。
所有这些工具都能有效地指引你决定接下来应该怎样做,让你把宝贵的时间用在刀刃上。现在你已经掌握了很多机器学习的工具,包括监督学习算法和无监督学习算法等等。
但除了这些以外,我更希望你现在不仅仅只是认识这些工具,更重要的是掌握怎样有效地利用这些工具来建立强大的机器学习系统。所以,以上就是这门课的全部内容。如果你跟着我们的课程一路走来,到现在,你应该已经感觉到自己已经成为机器学习方面的专家了吧?
我们都知道,机器学习是一门对科技、工业产生深远影响的重要学科,而现在,你已经完全具备了应用这些机器学习工具来创造伟大成就的能力。我希望你们中的很多人都能在相应的领域,应用所学的机器学习工具,构建出完美的机器学习系统,开发出无与伦比的产品和应用。并且我也希望你们通过应用机器学习,不仅仅改变自己的生活,有朝一日,还要让更多的人生活得更加美好!
我也想告诉大家,教这门课对我来讲是一种享受。所以,谢谢大家!
最后,在结束之前,我还想再多说一点:那就是,也许不久以前我也是一个学生,即使是现在,我也尽可能挤出时间听一些课,学一些新的东西。所以,我深知要坚持学完这门课是很需要花一些时间的,我知道,也许你是一个很忙的人,生活中有很多很多事情要处理。正因如此,你依然挤出时间来观看这些课程视频。我知道,很多视频的时间都长达数小时,你依然花了好多时间来做这些复习题。你们中好多人,还愿意花时间来研究那些编程练习,那些又长又复杂的编程练习。我对你们表示衷心的感谢!我知道你们很多人在这门课中都非常努力,很多人都在这门课上花了很多时间,很多人都为这门课贡献了自己的很多精力。所以,我衷心地希望你们能从这门课中有所收获!
最后我想说!再次感谢你们选修这门课程!
Andew Ng
其他
申请Coursera奖学金拿证书
I am a Master student at Shang Hai University which located in China,I’m so sorry I’m so poor to afford the cost in China All my income is just enough to cover my living expense, so I don’t have extra money to register the class. Furthermore, I want to save money for my family Since my parents have been working so hard to support me.For nowadays ,machine learning is so hot not only in China but also in the world I request Coursera for financial aid, and I promise I will finish the course in time. I think Coursera is a very good platform for people to learn something they need, and sincerely hoping to learn something. This program provided by Coursera is a great opportunity for a poor student like me to pursue the course, and I hope I can get the chance. Thank you for your consideration. I hope you can agree with my application. I look forward to your reply.Thank you so much
智能推荐
前端开发之vue-grid-layout的使用和实例-程序员宅基地
文章浏览阅读1.1w次,点赞7次,收藏34次。vue-grid-layout的使用、实例、遇到的问题和解决方案_vue-grid-layout
Power Apps-上传附件控件_powerapps点击按钮上传附件-程序员宅基地
文章浏览阅读218次。然后连接一个数据源,就会在下面自动产生一个添加附件的组件。把这个控件复制粘贴到页面里,就可以单独使用来上传了。插入一个“编辑”窗体。_powerapps点击按钮上传附件
C++ 面向对象(Object-Oriented)的特征 & 构造函数& 析构函数_"object(cnofd[\"ofdrender\"])十条"-程序员宅基地
文章浏览阅读264次。(1) Abstraction (抽象)(2) Polymorphism (多态)(3) Inheritance (继承)(4) Encapsulation (封装)_"object(cnofd[\"ofdrender\"])十条"
修改node_modules源码,并保存,使用patch-package打补丁,git提交代码后,所有人可以用到修改后的_修改 node_modules-程序员宅基地
文章浏览阅读133次。删除node_modules,重新npm install看是否成功。在 package.json 文件中的 scripts 中加入。修改你的第三方库的bug等。然后目录会多出一个目录文件。_修改 node_modules
【】kali--password:su的 Authentication failure问题,&sudo passwd root输入密码时Sorry, try again._password: su: authentication failure-程序员宅基地
文章浏览阅读883次。【代码】【】kali--password:su的 Authentication failure问题,&sudo passwd root输入密码时Sorry, try again._password: su: authentication failure
整理5个优秀的微信小程序开源项目_微信小程序开源模板-程序员宅基地
文章浏览阅读1w次,点赞13次,收藏97次。整理5个优秀的微信小程序开源项目。收集了微信小程序开发过程中会使用到的资料、问题以及第三方组件库。_微信小程序开源模板
随便推点
Centos7最简搭建NFS服务器_centos7 搭建nfs server-程序员宅基地
文章浏览阅读128次。Centos7最简搭建NFS服务器_centos7 搭建nfs server
Springboot整合Mybatis-Plus使用总结(mybatis 坑补充)_mybaitis-plus ruledataobjectattributemapper' and '-程序员宅基地
文章浏览阅读1.2k次,点赞2次,收藏3次。前言mybatis在持久层框架中还是比较火的,一般项目都是基于ssm。虽然mybatis可以直接在xml中通过SQL语句操作数据库,很是灵活。但正其操作都要通过SQL语句进行,就必须写大量的xml文件,很是麻烦。mybatis-plus就很好的解决了这个问题。..._mybaitis-plus ruledataobjectattributemapper' and 'com.picc.rule.management.d
EECE 1080C / Programming for ECESummer 2022 Laboratory 4: Global Functions Practice_eece1080c-程序员宅基地
文章浏览阅读325次。EECE 1080C / Programming for ECESummer 2022Laboratory 4: Global Functions PracticePlagiarism will not be tolerated:Topics covered:function creation and call statements (emphasis on global functions)Objective:To practice program development b_eece1080c
洛谷p4777 【模板】扩展中国剩余定理-程序员宅基地
文章浏览阅读53次。被同机房早就1年前就学过的东西我现在才学,wtcl。设要求的数为\(x\)。设当前处理到第\(k\)个同余式,设\(M = LCM ^ {k - 1} _ {i - 1}\) ,前\(k - 1\)个的通解就是\(x + i * M\)。那么其实第\(k\)个来说,其实就是求一个\(y\)使得\(x + y * M ≡ a_k(mod b_k)\)转化一下就是\(y * M ...
android 退出应用没有走ondestory方法,[Android基础论]为何Activity退出之后,系统没有调用onDestroy方法?...-程序员宅基地
文章浏览阅读1.3k次。首先,问题是如何出现的?晚上复查代码,发现一个activity没有调用自己的ondestroy方法我表示非常的费解,于是我检查了下代码。发现再finish代码之后接了如下代码finish();System.exit(0);//这就是罪魁祸首为什么这样写会出现问题System.exit(0);////看一下函数的原型public static void exit (int code)//Added ..._android 手动杀死app,activity不执行ondestroy
SylixOS快问快答_select函数 导致堆栈溢出 sylixos-程序员宅基地
文章浏览阅读894次。Q: SylixOS 版权是什么形式, 是否分为<开发版税>和<运行时版税>.A: SylixOS 是开源并免费的操作系统, 支持 BSD/GPL 协议(GPL 版本暂未确定). 没有任何的运行时版税. 您可以用她来做任何 您喜欢做的项目. 也可以修改 SylixOS 的源代码, 不需要支付任何费用. 当然笔者希望您可以将使用 SylixOS 开发的项目 (不需要开源)或对 SylixOS 源码的修改及时告知笔者.需要指出: SylixOS 本身仅是笔者用来提升自己水平而开发的_select函数 导致堆栈溢出 sylixos