更多文章可以在本人的个人小站：https://kaiserwilheim.github.io 查看。
转载请注明出处。

（3-13至3-14重修）
（6-23至6-24增添上下界网络流相关内容）

什么是网络流

网络流是指在网络（或者流网络， Flow Network ）中的流。

网络

网络是指一个有向图 $G=(V,E)$。

每条边 $(u,v)\in E$ 都有一个权值 $c(u,v)$，称之为容量（Capacity），当 $(u,v)\notin E$ 时有 $c(u,v)=0$。

其中有两个特殊的点：源点（Source）$s\in V$ 和汇点（Sink）$t\in V,(s\ne t)$。

流

设 $f(u,v)$ 定义在二元组 $(u\in V,v\in V)$ 上的实数函数且满足

1. 容量限制：对于每条边，流经该边的流量不得超过该边的容量，即，$f(u,v)\le c(u,v)$
2. 斜对称性：每条边的流量与其相反边的流量之和为 0，即 $f(u,v)=-f(v,u)$
3. 流守恒性：从源点流出的流量等于汇点流入的流量，即 ∀ x ∈ V − { s , t } , ∑ ( u , x ) ∈ E f ( u , x ) = ∑ ( x , v ) ∈ E f ( x , v ) \forall x\in V - \lbrace s,t \rbrace , \sum_{(u,x) \in E} f(u,x) = \sum_{(x,v) \in E} f(x,v) ∀x∈V−{ s,t},∑(u,x)∈E​f(u,x)=∑(x,v)∈E​f(x,v)

那么 $f$ 称为网络 $G$ 的流函数。对于 $(u,v)\in E$，$f(u,v)$ 称为边的流量，$c(u,v)-f(u,v)$ 称为边的剩余容量。整个网络的流量为 ${\sum }_{(s,v)\in E}f(s,v)$，即从源点发出的所有流量之和。

一般而言也可以把网络流理解为整个图的流量。而这个流量必满足上述三个性质。

流函数的完整定义为

$$f(u,v)=\{\begin{array}{ll}f(u,v),& (u,v)\in E,\\ & \\ -f(v,u),& (v,u)\in E,\\ & \\ 0,& (u,v)\notin E,(v,u)\notin E.\end{array}$$

反向边

反向边是网络流中很重要的一类边。

一般的时候，在题目给定的流网络中是不包含有关反向边的信息的，我们画图的时候也一般不将反向边画出来。

但是，反向边可以利用流网络的一些性质，通过对其流量进行操作，使得我们的子程序可以经由其进行反悔的操作。

建立反向边的时候可以使用一些小trick。

我们如果使用邻接表（或称链式前向星）来建图的话，可以选择同时建正向边和反向边，并使边的编号从0开始，从而可以通过使用异或操作来访问当前边的反向边。

网络流的常见问题

网络流问题中常见的有以下三种：最大流，最小割，费用流。

解决网络流问题的难点不是算法或者代码，而是建图。对于大多数的网络流题目，我们需要仔细分辨琢磨才可以知道如何将问题转换为网络流这几种问题的其中一种或几种，并将题目中的限制用边/点的限制体现出来。

最大流

简介

对于一个给定的网络，其合法的流函数其实有很多。其中使得整个网络的流量最大的流函数被称为网络的最大流。

求解一个网络的最大流其实有很多用处，例如可以将二分图的最大匹配问题转化为求解最大流。

求解最大流的算法有很多种，比如Ford-Fulkerson增广路算法、Push-Relable预流推进算法等等。
实际上，最常用的还是Ford-Fulkerson增广路算法中的EK和Dinic两种。

Ford-Fulkerson 增广路算法

该方法通过寻找增广路来更新最大流，有EK,dinic,SAP,ISAP等主流算法。

求解最大流之前，我们先认识一些概念。

残量网络

首先我们介绍一下一条边的剩余容量 $c_f(u,v)$（Residual Capacity），它表示的是这条边的容量与流量之差，即 $c_f(u,v)=c(u,v)-f(u,v)$。

对于流函数 $f$，残存网络 $G_f$（Residual Network）是网络 $G$ 中所有结点和剩余容量大于 0 的边构成的子图。形式化的定义，即 G f = ( V f = V , E f = { ( u , v ) ∈ E , c f ( u , v ) > 0 } ) G_f = (V_f = V,E_f = \lbrace(u,v) \in E,c_f(u,v) > 0 \rbrace) Gf​=(Vf​=V,Ef​={ (u,v)∈E,cf​(u,v)>0})。

注意，剩余容量大于 0 的边可能不在原图 $G$ 中（根据容量、剩余容量的定义以及流函数的斜对称性得到）。可以理解为，残量网络中包括了那些还剩了流量空间的边构成的图，也包括虚边（即反向边）。

增广路

在原图 $G$ 中若一条从源点到汇点的路径上所有边的剩余容量都大于 0，这条路被称为增广路（Augmenting Path）。

或者说，在残存网络 $G_f$ 中，一条从源点到汇点的路径被称为增广路。如图：

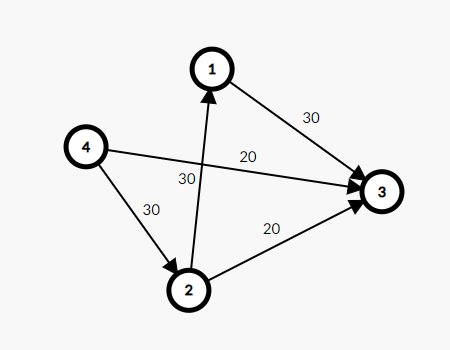
我们从 $4$ 到 $3$，肯定可以先从流量为 $20$ 的这条边先走。那么这条边就被走掉了，不能再选，总的流量为 $20$（现在）。然后我们可以这样选择：

1. $4\to 2\to 3$ 这条 增广路 的总流量为 $20$。到 $2$ 的时候还是 $30$，到 $3$ 了就只有 $20$ 了。

2. $4\to 2\to 1\to 3$ 这样子我们就很好的保留了 $30$ 的流量。

所以我们这张图的最大流就应该是 $20+30=50$。

Edmonds-Karp 动能算法

这个算法很简单，就是BFS找增广路，然后对其进行增广，直到图上再也没有增广路了为止。

我们不用管我们找到的增广路的正确性，毕竟如果我们找到了一条更优的路径的话可以通过之前经过的反向边进行反悔。这也就意味着，我们每次需要BFS的边鸡是包括反向边的。

在具体实现的时候，我们每一次找到增广路的时候，记录下这条路径上所有的最小流量 $minf$ ，那么整个图的流量就增加了 $minf$。同时我们给这条路径上的所有边的反向边都加上 $minf$ 的容量，以便将来反悔。

EK 算法的时间复杂度为 $O(n{m}^2)$（其中 $n$ 为点数，$m$ 为边数）。
其效率还有很大提升空间，但实际情况下不一定能跑满，应付 $10^3\sim 10^4$ 大小的图应该足够了。

参考代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 1010, M = 20010, INF = 1e8;
int n, m, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], pre[N];
bool st[N];

void add(int a, int b, int c)
{
    
	e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx++;
	e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx++;
}

bool bfs()
{
    
	int hh = 0, tt = 0;
	memset(st, false, sizeof(st));
	q[0] = S, st[S] = true, d[S] = INF;
	while(hh <= tt)
	{
    
		int t = q[hh++];
		for(int i = h[t]; ~i; i = ne[i])
		{
    
			int ver = e[i];
			if(!st[ver] && f[i])
			{
    
				st[ver] = true;
				d[ver] = min(d[t], f[i]);
				pre[ver] = i;
				if(ver == T) return true;
				q[++tt] = ver;
			}
		}
	}
	return false;
}

int EK()
{
    
	int r = 0;
	while(bfs())
	{
    
		r += d[T];
		for(int i = T; i != S; i = e[pre[i] ^ 1])
			f[pre[i]] -= d[T], f[pre[i] ^ 1] += d[T];
	}
	return r;
}

int main()
{
    
	scanf("%d%d%d%d", &n, &m, &S, &T);
	memset(h, -1, sizeof(h));
	while(m--)
	{
    
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		add(a, b, c);
	}
	printf("%d\n", EK());
	return 0;
}

Dinic 算法

EK 算法每一次遍历残量网络的时候只能最多找到一条增广路，但很可能我们的子程序为此而遍历了整个残量网络。这里还有很大的优化空间。

Dinic 算法的过程是这样的：每次增广前，我们先用 BFS 来将图分层。设源点的层数为 $0$，那么一个点的层数便是它离源点的最近距离。

通过分层，我们可以干两件事情：

1. 如果不存在到汇点的增广路（即汇点的层数不存在），我们即可停止增广。
2. 确保我们找到的增广路是最短的。（原因见下文）

接下来是 DFS 找增广路的过程。

我们每次找增广路的时候，都只找比当前点层数多 $1$ 的点进行增广（这样就可以确保我们找到的增广路是最短的）。

Dinic 算法会不断重复这两个过程，直到没有增广路了为止。

Dinic 算法有两个优化：

1. 多路增广：每次找到一条增广路的时候，如果残余流量没有用完怎么办呢？我们可以利用残余部分流量，再找出一条增广路。这样就可以在一次 DFS 中找出多条增广路，大大提高了算法的效率。
2. 当前弧优化：如果一条边已经被增广过，那么它就没有可能被增广第二次。那么，我们下一次进行增广的时候，就可以不必再走那些已经被增广过的边。

Dinic 算法的时间复杂度是 $O(n^{2}m)$ 级别的，但实际上其实跑不满这个上限。
Dinic算法可以说是算法实现难易程度与时间复杂度较为平衡的一个算法，可以应对 $10^4\sim 10^5$级别的图。
特别的，Dinic算法在求解二分图最大匹配问题的时候的时间复杂度是 $O(m\sqrt{n})$ 级别的，实际情况下则比这更优。

参考代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 10010, M = 200010, INF = 1e8;
int n, m, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], cur[N];

void add(int a, int b, int c)
{
    
	e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx++;
	e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx++;
}

bool bfs()
{
    
	int hh = 0, tt = 0;
	memset(d, -1, sizeof(d));
	q[0] = S, d[S] = 0, cur[S] = h[S];
	while(hh <= tt)
	{
    
		int u = q[hh++];
		for(int i = h[u]; ~i; i = ne[i])
		{
    
			int v = e[i];
			if(d[v] == -1 && f[i])
			{
    
				d[v] = d[u] + 1;
				cur[v] = h[v];
				if(v == T)return true;
				q[++tt] = v;
			}
		}
	}
	return false;
}

int find(int u, int limit)
{
    
	if(u == T)return limit;
	int flow = 0;
	for(int i = cur[u]; ~i && flow < limit; i = ne[i])
	{
    
		cur[u] = i;//当前弧优化
		int v = e[i];
		if(d[v] == d[u] + 1 && f[i])
		{
    
			int t = find(v, min(f[i], limit - flow));
			if(!t)d[v] = -1;
			f[i] -= t, f[i ^ 1] += t;
			flow += t;
		}
	}
	return flow;
}

int dinic()
{
    
	int r = 0, flow;
	while(bfs()) while(flow = find(S, INF)) r += flow;
	return r;
}

int main()
{
    
	scanf("%d%d%d%d", &n, &m, &S, &T);
	memset(h, -1, sizeof(h));
	while(m--)
	{
    
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		add(a, b, c);
	}
	printf("%d\n", dinic());
	return 0;
}

最小割

简介

对于一个给定的网络，我们删去网络中的一个边集，使得源点与汇点不连通，这个被删去的边集就是这张图的一个割。在所有的割中，边集的容量和最小的被称为最小割。

最大流最小割定理

任何一个网络的最大流量等于最小割中边的容量值和。

证明

我们如果回想一下最大流算法走完之后的结果。

对于每一条从源点到汇点的流量为正的路径，我们都能找到至少一条容量跑满的边。

这些边的容量之和就是我们最终得到的最大流。

我们考虑将这些边删去。

那么我们如果对剩下的边跑最大流算法的话，我们得到的最大流将会是0，也就意味着源点将不再与汇点直接连通。

这些跑满的边构成的边集就满足了我们对割的定义。

实现

所以说，我们完全可以用求解最大流的算法来求解最小割问题。

费用流

简介

给定一个网络 $G=(V,E)$，每条边除了有容量限制 $c(u,v)$，还有一个单位流量的费用 $w(u,v)$。

当 $(u,v)$ 的流量为 $f(u,v)$ 时，需要花费 $f(u,v)\times w(u,v)$ 的费用。

$w$ 也满足斜对称性，即 $w(u,v)=-w(v,u)$。

则该网络中总花费最小的最大流称为最小费用最大流，即在最大化 ${\sum }_{(s,v)\in E}f(s,v)$ 的前提下最小化 ${\sum }_{(u,v)\in E}f(u,v)\times w(u,v)$。

最小费用最大流问题与带权二分图最大匹配问题的关系就和最大流问题和二分图最大匹配问题的关系类似，这就意味着我们可以使用求解费用流问题的算法来求解带权二分图最大匹配问题。

SSP 算法

SSP（Successive Shortest Path）算法是一个贪心的算法。它的思路是每次寻找单位费用最小的增广路进行增广，直到图上不存在增广路为止。

如果图上存在单位费用为负的圈，SSP 算法正确无法求出该网络的最小费用最大流。此时需要先使用消圈算法消去图上的负圈。

时间复杂度

如果使用 Bellman-Ford 算法求解最短路，每次找增广路的时间复杂度为 $O(nm)$。设该网络的最大流为 $f$，则最坏时间复杂度为 $O(nmf)$。事实上，这个时间复杂度是伪多项式的。

实现

只需将 EK 算法或 Dinic 算法中找增广路的过程，替换为用最短路算法寻找单位费用最小的增广路即可。

这里写的是SPFA，因为怕有负边权导致的奇怪的结果。

当然，如果没有负权的话可以使用dijkstra。

基于EK算法的实现：

#include<bits/stdc++.h>
using namespace std;
const int N = 5010, M = 100010, INF = 1e8;
int n, m, S, T;
int h[N], e[M], f[M], w[M], ne[M], idx;
int q[N], d[N], pre[N], incf[N];
bool st[N];

void add(int a, int b, int c, int d)
{
    
	e[idx] = b, f[idx] = c, w[idx] = d, ne[idx] = h[a], h[a] = idx++;
	e[idx] = a, f[idx] = 0, w[idx] = -d, ne[idx] = h[b], h[b] = idx++;
}

bool spfa()
{
    
	int hh = 0, tt = 1;
	memset(d, 0x3f, sizeof(d));
	memset(incf, 0, sizeof(incf));
	q[0] = S, d[S] = 0, incf[S] = INF;
	while(hh != tt)
	{
    
		int t = q[hh++];
		if(hh == N) hh = 0;
		st[t] = false;

		for(int i = h[t]; ~i; i = ne[i])
		{
    
			int ver = e[i];
			if(f[i] && d[ver] > d[t] + w[i])
			{
    
				d[ver] = d[t] + w[i];
				pre[ver] = i;
				incf[ver] = min(f[i], incf[t]);
				if(!st[ver])
				{
    
					q[tt++] = ver;
					if(tt == N) tt = 0;
					st[ver] = true;
				}
			}
		}
	}

	return incf[T] > 0;
}

void EK(int &flow, int &cost)
{
    
	flow = cost = 0;
	while(spfa())
	{
    
		int t = incf[T];
		flow += t, cost += t * d[T];
		for(int i = T; i != S; i = e[pre[i] ^ 1])
		{
    
			f[pre[i]] -= t;
			f[pre[i] ^ 1] += t;
		}
	}
}

int main()
{
    
	scanf("%d%d%d%d", &n, &m, &S, &T);
	memset(h, -1, sizeof(h));
	while(m--)
	{
    
		int a, b, c, d;
		scanf("%d%d%d%d", &a, &b, &c, &d);
		add(a, b, c, d);
	}
	int flow, cost;
	EK(flow, cost);
	printf("%d %d\n", flow, cost);
	return 0;
}

上下界网络流

现在我们每一条边不仅有流量的上界了，还有了流量的下界。

无源汇有上下界可行流

现在我们手里拿到了一张图，上面没有给定源点和汇点，同时每一条边都有流量的上界和下界。
现在我们需要求出来一个方案，使得我们这张图的所有点满足流量平衡（即每一个点流出的流量和流入的流量是相等的），同时满足流量限制。

例题就是LibreOJ的#115. 无源汇有上下界可行流。

我们的思路如下：

我们可以将我们的一个可行方案拆成两部分，为每一条边的下限加上超出每一条边下限的部分。
我们称超出每一条边下限的这部分流叫做附加流。

首先我们跑满所有边的下限，记录下每一个点流入流量与流出流量之差，设其为 $A_i$。

根据上面我们得到的信息，我们在建立一个新图，是正常的不带下界的网络流，并新建两个源汇点 $S$ 与 $T$。这张图里面的边与原先起始点一样，而流量变为了原边的上界减去下界。

因为部分点的流量不是平衡的，我们需要让其在加上附加流之后平衡，同时在求附加流的这个图中也需要保证流量平衡，所以我们需要将每一个点中不平衡的流量给到源点或汇点。

对于 $A_i>0$ 的，说明这个点流入较多，需要往出流，其附加流的流出流量是大于其流入流量的，所以需要从 $S$ 向其连一条流量为 $A_i$ 的边；
对于 $A_i<0$ 的，说明这个点流出较多，需要再流入，其附加流的流入流量是大于其流出流量的，所以需要从其向 $T$ 连一条流量为 $-A_i$ 的边。

我们对这个新图跑一个最大流，然后看起最大流量是否等于 $S$ 的所有出边流量之和。如果相等，那么原图也就流量平衡了，这时候我们就得到了一个可行的方案。

参考代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 100010, M = 200010;
const int INF = 1e9;
int m, n;
int S, T;
int h[N], e[M], ne[M], f[M], l[M], idx;
int A[N];
int q[N], d[N], cur[N];
void add(int a, int b, int c, int d)
{
    
	e[idx] = b, ne[idx] = h[a], f[idx] = d - c, l[idx] = c, h[a] = idx++;
	e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx++;
}
bool bfs()
{
    
	int hh = 0, tt = 0;
	memset(d, -1, sizeof(d));
	q[0] = S, d[S] = 0, cur[S] = h[S];
	while(hh <= tt)
	{
    
		int u = q[hh++];
		for(int i = h[u]; ~i; i = ne[i])
		{
    
			int v = e[i];
			if(d[v] == -1 && f[i])
			{
    
				d[v] = d[u] + 1;
				cur[v] = h[v];
				if(v == T)return true;
				q[++tt] = v;
			}
		}
	}
	return false;
}
int find(int u, int limit)
{
    
	if(u == T)return limit;
	int flow = 0;
	for(int i = cur[u]; ~i && flow < limit; i = ne[i])
	{
    
		cur[u] = i;
		int v = e[i];
		if(d[v] == d[u] + 1 && f[i])
		{
    
			int t = find(v, min(f[i], limit - flow));
			if(!t)d[v] = -1;
			f[i] -= t, f[i ^ 1] += t;
			flow += t;
		}
	}
	return flow;
}
int dinic()
{
    
	int r = 0, flow;
	while(bfs())while(flow = find(S, INF))r += flow;
	return r;
}
int main()
{
    
	memset(h, -1, sizeof(h));
	scanf("%d%d", &n, &m);
	S = 0, T = n + 1;
	for(int i = 1; i <= m; i++)
	{
    
		int a, b, c, d;
		scanf("%d%d%d%d", &a, &b, &c, &d);
		add(a, b, c, d);
		A[a] -= c, A[b] += c;
	}
	int tot = 0;
	for(int i = 1; i <= n; i++)
	{
    
		if(A[i] > 0)
		{
    
			add(S, i, 0, A[i]);
			tot += A[i];
		}
		else if(A[i] < 0)
		{
    
			add(i, T, 0, -A[i]);
		}
	}
	int res = dinic();
	if(res != tot)puts("NO");
	else
	{
    
		puts("YES");
		for(int i = 0; i < m * 2; i += 2)
			printf("%d\n", f[i ^ 1] + l[i]);
	}
	return 0;
}

有源汇有上下界最大/最小流

我们知道，在一个图中要能够跑出一个可行流的前提是所有点都需要流量平衡，但是我们的源点和汇点都没有流量平衡，这就很难办。

一个可以想到的方法就是，从汇点向源点连接一条容量为无限的边，这样就可以跑出来一个可行流。

我们再从给定的源点到汇点再跑一个最大流，将其加到我们的可行流上面就是我们的最大流了；
如果想要求最小流的话，就可以从汇点到源点跑一个残量网络上的最大流，代表着我们可以将这些流回退掉，从可行流里面减去当前的最大流就是最小流了。

例题分别是LibreOJ的#116. 有源汇有上下界最大流和#117. 有源汇有上下界最小流。

最大流 参考代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 100010, M = 200010;
const int INF = 1e9;
int m, n;
int S, T, s, t;
int h[N], e[M], ne[M], f[M], l[M], idx;
int A[N];
int q[N], d[N], cur[N];
void add(int a, int b, int c, int d)
{
    
	e[idx] = b, ne[idx] = h[a], f[idx] = d - c, l[idx] = c, h[a] = idx++;
	e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx++;
}
bool bfs()
{
    
	int hh = 0, tt = 0;
	memset(d, -1, sizeof(d));
	q[0] = S, d[S] = 0, cur[S] = h[S];
	while(hh <= tt)
	{
    
		int u = q[hh++];
		for(int i = h[u]; ~i; i = ne[i])
		{
    
			int v = e[i];
			if(d[v] == -1 && f[i])
			{
    
				d[v] = d[u] + 1;
				cur[v] = h[v];
				if(v == T)return true;
				q[++tt] = v;
			}
		}
	}
	return false;
}
int find(int u, int limit)
{
    
	if(u == T)return limit;
	int flow = 0;
	for(int i = cur[u]; ~i && flow < limit; i = ne[i])
	{
    
		cur[u] = i;
		int v = e[i];
		if(d[v] == d[u] + 1 && f[i])
		{
    
			int t = find(v, min(f[i], limit - flow));
			if(!t)d[v] = -1;
			f[i] -= t, f[i ^ 1] += t;
			flow += t;
		}
	}
	return flow;
}
int dinic()
{
    
	int r = 0, flow;
	while(bfs())while(flow = find(S, INF))r += flow;
	return r;
}
int main()
{
    
	memset(h, -1, sizeof(h));
	scanf("%d%d", &n, &m);
	scanf("%d%d", &s, &t);
	S = 0, T = n + 1;
	for(int i = 1; i <= m; i++)
	{
    
		int a, b, c, d;
		scanf("%d%d%d%d", &a, &b, &c, &d);
		add(a, b, c, d);
		A[a] -= c, A[b] += c;
	}
	int tot = 0;
	for(int i = 1; i <= n; i++)
	{
    
		if(A[i] > 0)
		{
    
			add(S, i, 0, A[i]);
			tot += A[i];
		}
		else if(A[i] < 0)
		{
    
			add(i, T, 0, -A[i]);
		}
	}
	add(t, s, 0, INF);
	int res = dinic();
	if(res != tot)puts("please go home to sleep");
	else
	{
    
		res = f[idx - 1];
		f[idx - 1] = f[idx - 2] = 0;
		S = s, T = t;
		int ans = res + dinic();
		printf("%d\n", ans);
	}
	return 0;
}

最小流 参考代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 100010, M = 400010;
const int INF = 1e9;
int m, n;
int S, T, s, t;
int h[N], e[M], ne[M], f[M], l[M], idx;
int A[N];
int q[N], d[N], cur[N];
void add(int a, int b, int c, int d)
{
    
	e[idx] = b, ne[idx] = h[a], f[idx] = d - c, l[idx] = c, h[a] = idx++;
	e[idx] = a, ne[idx] = h[b], f[idx] = 0, h[b] = idx++;
}
bool bfs()
{
    
	int hh = 0, tt = 0;
	memset(d, -1, sizeof(d));
	q[0] = S, d[S] = 0, cur[S] = h[S];
	while(hh <= tt)
	{
    
		int u = q[hh++];
		for(int i = h[u]; ~i; i = ne[i])
		{
    
			int v = e[i];
			if(d[v] == -1 && f[i])
			{
    
				d[v] = d[u] + 1;
				cur[v] = h[v];
				if(v == T)return true;
				q[++tt] = v;
			}
		}
	}
	return false;
}
int find(int u, int limit)
{
    
	if(u == T)return limit;
	int flow = 0;
	for(int i = cur[u]; ~i && flow < limit; i = ne[i])
	{
    
		cur[u] = i;
		int v = e[i];
		if(d[v] == d[u] + 1 && f[i])
		{
    
			int t = find(v, min(f[i], limit - flow));
			if(!t)d[v] = -1;
			f[i] -= t, f[i ^ 1] += t;
			flow += t;
		}
	}
	return flow;
}
int dinic()
{
    
	int r = 0, flow;
	while(bfs())while(flow = find(S, INF))r += flow;
	return r;
}
int main()
{
    
	memset(h, -1, sizeof(h));
	scanf("%d%d", &n, &m);
	scanf("%d%d", &s, &t);
	S = 0, T = n + 1;
	for(int i = 1; i <= m; i++)
	{
    
		int a, b, c, d;
		scanf("%d%d%d%d", &a, &b, &c, &d);
		add(a, b, c, d);
		A[a] -= c, A[b] += c;
	}
	int tot = 0;
	for(int i = 1; i <= n; i++)
	{
    
		if(A[i] > 0)
		{
    
			add(S, i, 0, A[i]);
			tot += A[i];
		}
		else if(A[i] < 0)
		{
    
			add(i, T, 0, -A[i]);
		}
	}
	add(t, s, 0, INF);
	int res = dinic();
	if(res != tot)puts("please go home to sleep");
	else
	{
    
		res = f[idx - 1];
		f[idx - 1] = f[idx - 2] = 0;
		S = t, T = s;
		int ans = res - dinic();
		printf("%d\n", ans);
	}
	return 0;
}