null - 程序员宅基地

如何理解最小二乘法？-程序员宅基地

最小平方法是十九世纪统计学的主题曲。从许多方面来看, 它之于统计学就相当于十八世纪的微积分之于数学。
----乔治·斯蒂格勒的《The History of Statistics》

1 日用而不知

来看一个生活中的例子。比如说，有五把尺子：

用它们来分别测量一线段的长度，得到的数值分别为（颜色指不同的尺子）：

$\begin{array}{c|c} \qquad\qquad&\qquad长度\qquad\\\hline \color{red}红& 10.2 \\\hline \color{blue}蓝& 10.3 \\\hline \color{orange}橙&9.8\\\hline \color{Goldenrod}黄&9.9\\\hline \color{green}绿&9.8\\\end{array}$

之所以出现不同的值可能因为：

不同厂家的尺子的生产精度不同
尺子材质不同，热胀冷缩不一样
测量的时候心情起伏不定
......

总之就是有误差，这种情况下，一般取平均值来作为线段的长度：

$\overline{x}=\frac{10.2+10.3+9.8+9.9+9.8}{5}=10$

日常中就是这么使用的。可是作为很事'er的数学爱好者，自然要想下：

这样做有道理吗？
用调和平均数行不行？
用中位数行不行？
用几何平均数行不行？

2 最小二乘法

换一种思路来思考刚才的问题。

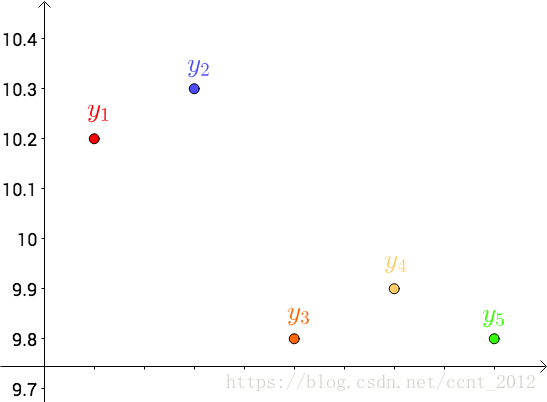
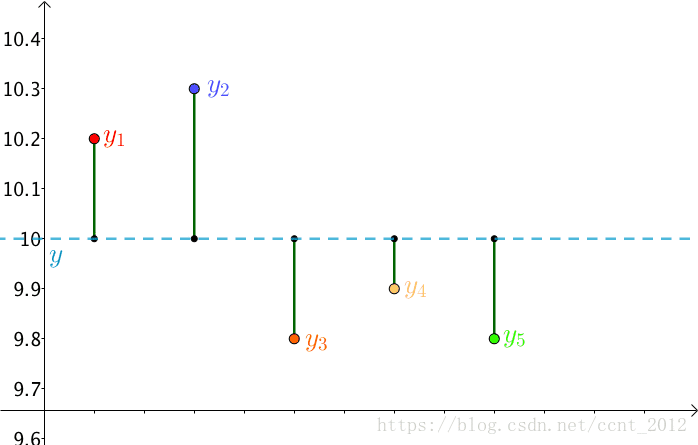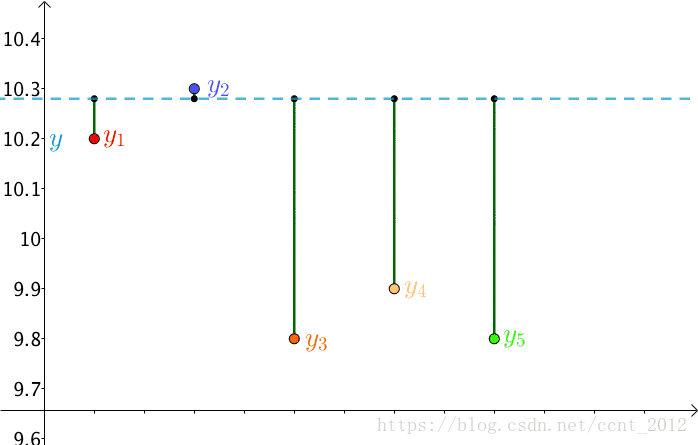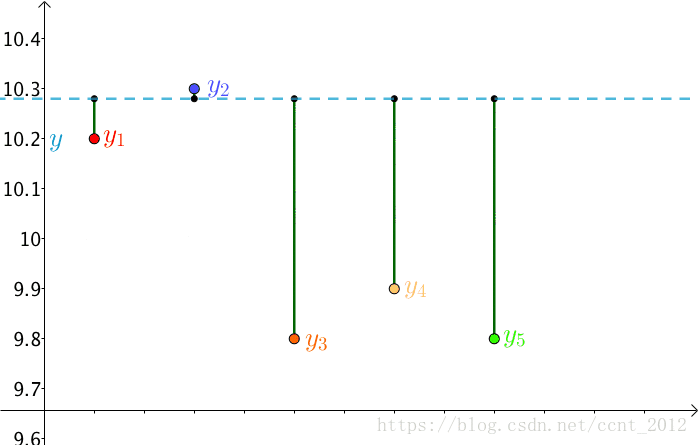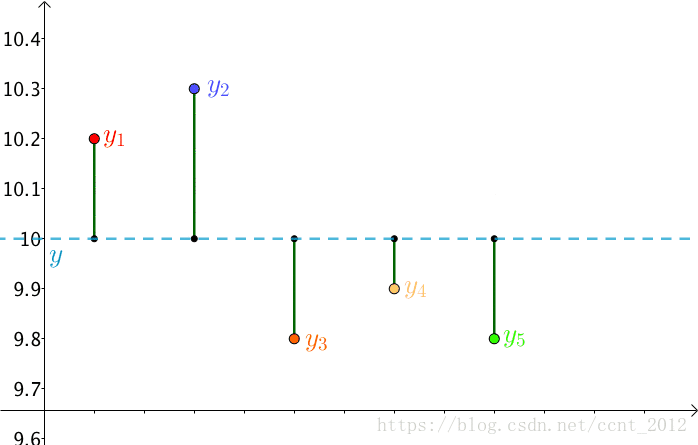
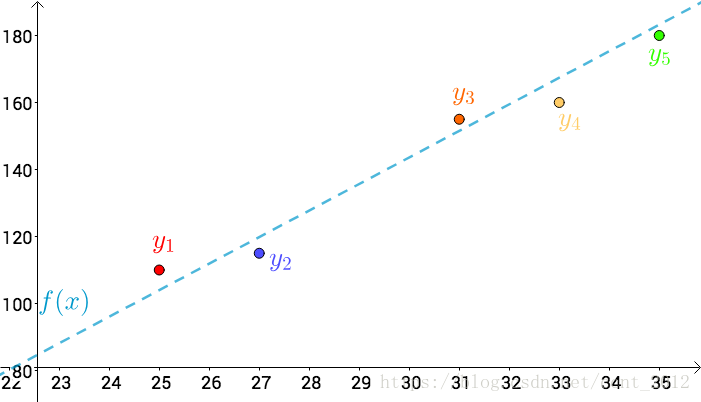
首先，把测试得到的值画在笛卡尔坐标系中，分别记作 $y_i$ ：

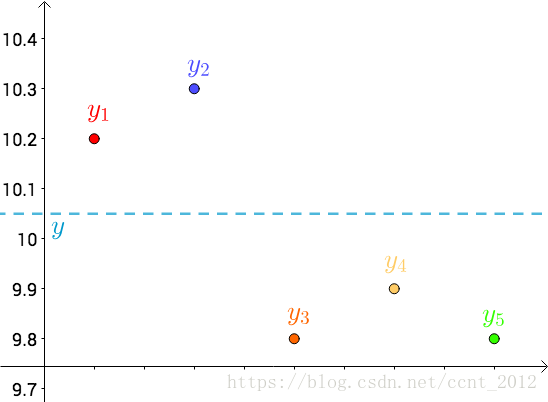
其次，把要猜测的线段长度的真实值用平行于横轴的直线来表示（因为是猜测的，所以用虚线来画），记作 $y$ ：

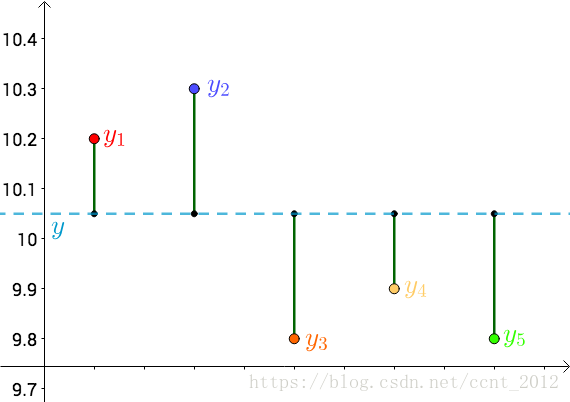
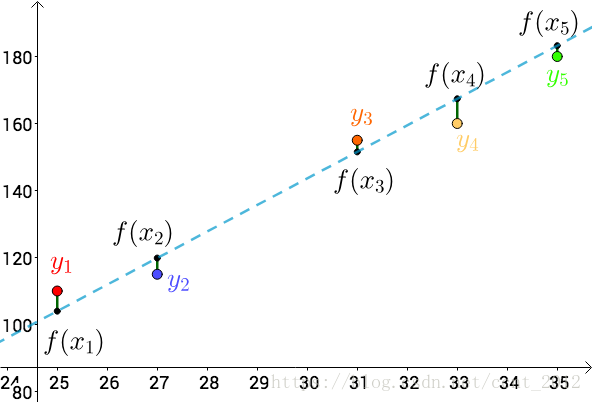
每个点都向 $y$ 做垂线，垂线的长度就是 $|y-y_i|$ ，也可以理解为测量值和真实值之间的误差：

因为误差是长度，还要取绝对值，计算起来麻烦，就干脆用平方来代表误差：

$|y-y_i|\to (y-y_i)^2$

总的误差的平方就是：

$\epsilon=\sum (y-y_i)^2$

因为 $y$ 是猜测的，所以可以不断变换：

自然，总的误差 $\epsilon$ 也是在不断变化的。

法国数学家，阿德里安-馬里·勒讓德（1752－1833，这个头像有点抽象）提出让总的误差的平方最小的 $y$ 就是真值，这是基于，如果误差是随机的，应该围绕真值上下波动（关于这点可以看下“如何理解无偏估计？”）。

这就是最小二乘法，即：

$\epsilon=\sum (y-y_i)^2最小\implies 真值y$

这个猜想也蛮符合直觉的，来算一下。

这是一个二次函数，对其求导，导数为0的时候取得最小值：

$\begin{aligned} \frac{d}{dy}\epsilon &=\frac{d}{dy}\sum (y-y_i)^2=2\sum (y-y_i)\\ \quad\\ &=2((y-y_1)+(y-y_2)+(y-y_3)+(y-y_4)+(y-y_5))=0 \quad\\\end{aligned}$

进而：

$5y=y_1+y_2+y_3+y_4+y_5\implies y=\frac{y_1+y_2+y_3+y_4+y_5}{5}$

正好是算术平均数。

原来算术平均数可以让误差最小啊，这下看来选用它显得讲道理了。

以下这种方法：

$\epsilon=\sum (y-y_i)^2最小\implies 真值y$

就是最小二乘法，所谓“二乘”就是平方的意思，台湾直接翻译为最小平方法。

3 推广

算术平均数只是最小二乘法的特例，适用范围比较狭窄。而最小二乘法用途就广泛。

比如温度与冰淇淋的销量：

$\begin{array}{c|c} \qquad\qquad&\qquad销量\qquad\\\hline \color{red}{25^\circ}& 110 \\\hline \color{blue}{27^\circ}& 115 \\\hline \color{orange}{31^\circ}&155\\\hline \color{Goldenrod}{33^\circ}&160\\\hline \color{green}{35^\circ}&180\\\end{array}$

看上去像是某种线性关系：

可以假设这种线性关系为：

$f(x)=ax+b$

通过最小二乘法的思想：

上图的 $i,x,y$ 分别为：

$\begin{array}{c|c|c} \qquad i\qquad&\qquad x\qquad&\qquad y\qquad\\\hline 1&25& 110 \\\hline 2&27& 115 \\\hline 3&31&155\\\hline 4&33&160\\\hline 5&35&180\\\end{array}$

总误差的平方为：

$\epsilon=\sum (f(x_i)-y_i)^2=\sum (ax_i+b-y_i)^2$

不同的 $a,b$ 会导致不同的 $\epsilon$ ，根据多元微积分的知识，当：

$\begin{cases} \frac{\partial}{\partial a}\epsilon=2\sum (ax_i+b-y_i)x_i=0\\ \quad\\ \frac{\partial}{\partial b}\epsilon=2\sum (ax_i+b-y_i)=0\end{cases}$

这个时候 $\epsilon$ 取最小值。

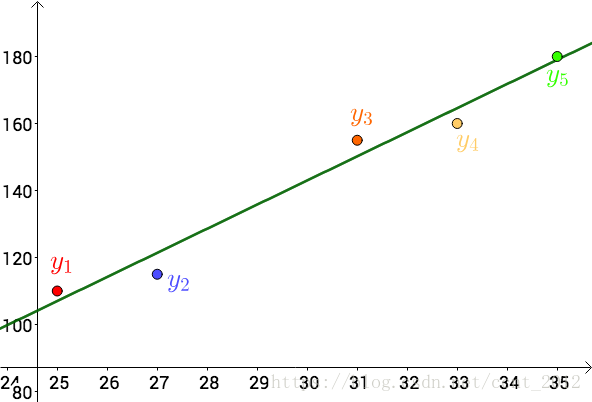
对于 $a,b$ 而言，上述方程组为线性方程组，用之前的数据解出来：

$\begin{cases} a\approx 7.2\\ \quad\\ b\approx -73\end{cases}$

也就是这根直线：

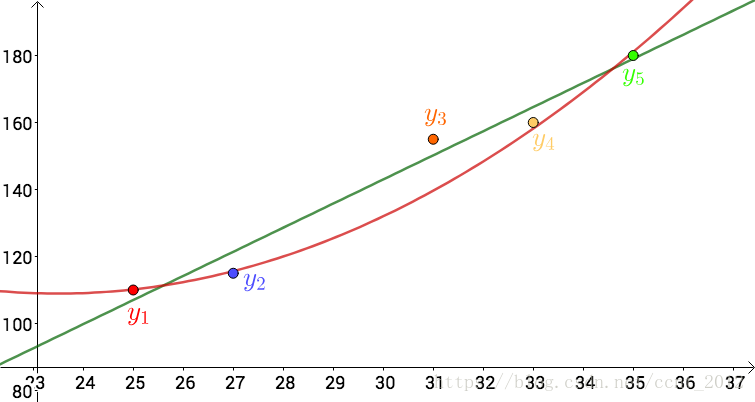
其实，还可以假设：

$f(x)=ax^2+bx+c$

在这个假设下，可以根据最小二乘法，算出 $a,b,c$ ，得到下面这根红色的二次曲线：

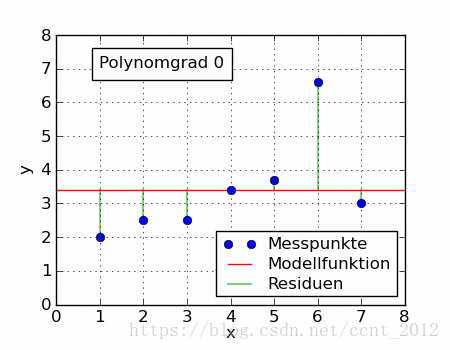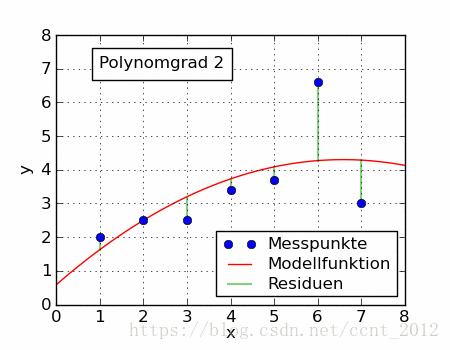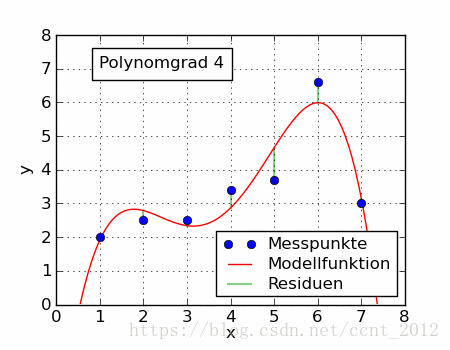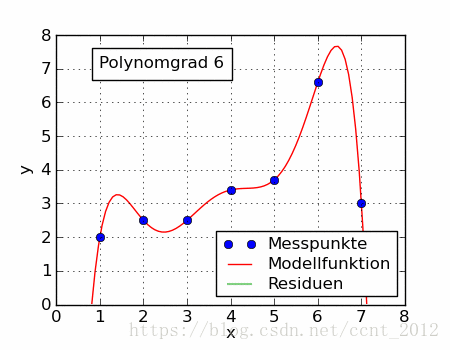
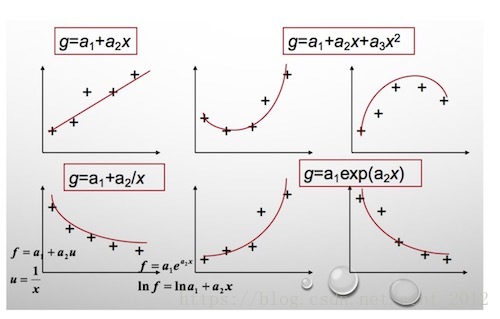
同一组数据，选择不同的 $f(x)$ ，通过最小二乘法可以得到不一样的拟合曲线（出处）：

不同的数据，更可以选择不同的 $f(x)$ ，通过最小二乘法可以得到不一样的拟合曲线：

$f(x)$ 也不能选择任意的函数，还是有一些讲究的，这里就不介绍了。

4 最小二乘法与正态分布

我们对勒让德的猜测，即最小二乘法，仍然抱有怀疑，万一这个猜测是错误的怎么办？

数学王子高斯（1777－1855）也像我们一样心存怀疑。

高斯换了一个思考框架，通过概率统计那一套来思考。

让我们回到最初测量线段长度的问题。高斯想，通过测量得到了这些值：

每次的测量值 $x_i$ 都和线段长度的真值 $x$ 之间存在一个误差：

$\epsilon_i=x-x_i$

这些误差最终会形成一个概率分布，只是现在不知道误差的概率分布是什么。假设概率密度函数为：

$p(\epsilon)$

再假设一个联合概率密度函数，这样方便把所有的测量数据利用起来：

$\begin{aligned} L(x) &=p(\epsilon_1)p(\epsilon_2)\cdots p(\epsilon_5)\\ \quad\\ &=p(x-x_i)p(x-x_2)\cdots p(x-x_5)\end{aligned}$

讲到这里，有些同学可能已经看出来了上面似然函数了（关于似然函数以及马上要讲到的极大似然估计，可以参考“如何理解极大似然估计法？”）。

因为 $L(x)$ 是关于 $x$ 的函数，并且也是一个概率密度函数（下面分布图形是随便画的）：

根据极大似然估计的思想，概率最大的最应该出现（既然都出现了，而我又不是“天选之才”，那么自然不会是发生了小概率事件），也就是应该取到下面这点：

当下面这个式子成立时，取得最大值：

$\frac{d}{dx}L(x)=0$

然后高斯想，最小二乘法给出的答案是：

$x=\overline{x}=\frac{x_1+x_2+x_3+x_4+x_5}{5}$

如果最小二乘法是对的，那么 $x=\overline{x}$ 时应该取得最大值，即：

$\frac{d}{dx}L(x)|_{x=\overline{x}}=0$

好，现在可以来解这个微分方程了。最终得到：

$p(\epsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\epsilon^2 \over 2\sigma^2}}}$

这是什么？这就是正态分布啊。

并且这还是一个充要条件：

$x=\overline{x}\iff p(\epsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\epsilon^2 \over 2\sigma^2}}}$

也就是说，如果误差的分布是正态分布，那么最小二乘法得到的就是最有可能的值。

那么误差的分布是正态分布吗？

我们相信，误差是由于随机的、无数的、独立的、多个因素造成的，比如之前提到的：

不同厂家的尺子的生产精度不同
尺子材质不同，热胀冷缩不一样
测量的时候心情起伏不定
......

那么根据中心极限定理（参考“为什么正态分布如此常见？”），误差的分布就应该是正态分布。

因为高斯的努力，才真正奠定了最小二乘法的重要地位。

文章最新版本在（有可能会有后续更新）：如何理解最小二乘法？

本文链接：https://blog.csdn.net/ccnt_2012/article/details/81127117

原作者删帖不实内容删帖广告或垃圾文章投诉

智能推荐

如何配置filezilla服务端和客户端_filezilla server for windows (32bit x86)-程序员宅基地

文章浏览阅读7.8k次，点赞3次，收藏9次。如何配置filezilla服务端和客户端百度‘filezilla server’下载最新版。注意点：下载的版本如果是32位的适用xp和win2003，百度首页的是适用于win7或更高的win系统。32和64内容无异。安装过程也是一样的。一、这里的filezilla包括服务端和客户端。我们先来用filezilla server 架设ftp服务端。看步骤。1选择标准版的就可以了。 _filezilla server for windows (32bit x86)

深度学习图像处理01：图像的本质-程序员宅基地

文章浏览阅读724次，点赞18次，收藏8次。深度学习作为一种强大的机器学习技术，已经成为图像处理领域的核心技术之一。通过模拟人脑处理信息的方式，深度学习能够从图像数据中学习到复杂的模式和特征，从而实现从简单的图像分类到复杂的场景理解等多种功能。要充分发挥深度学习在图像处理中的潜力，我们首先需要理解图像的本质。本文旨在深入探讨深度学习图像处理的基础概念，为初学者铺平通往高级理解的道路。我们将从最基础的问题开始：图像是什么？我们如何通过计算机来理解和处理图像？

数据探索阶段——对样本数据集的结构和规律进行分析_数据分析规律集-程序员宅基地

文章浏览阅读62次。在收集到初步的样本数据之后，接下来该考虑的问题有：（1）样本数据集的数量和质量是否满足模型构建的要求。（2）是否出现从未设想过的数据状态。（3）是否有明显的规律和趋势。（4）各因素之间有什么样的关联性。解决方案：检验数据集的数据质量、绘制图表、计算某些特征量等，对样本数据集的结构和规律进行分析。从数据质量分析和数据特征分析两个角度出发。_数据分析规律集

上传计算机桌面文件图标不见,关于桌面上图标都不见了这类问题的解决方法-程序员宅基地

文章浏览阅读8.9k次。关于桌面上图标都不见了这类问题的解决方法1、在桌面空白处右击鼠标-->排列图标-->勾选显示桌面图标。2、如果问题还没解决，那么打开任务管理器(同时按“Ctrl+Alt+Del”即可打开)，点击“文件”→“新建任务”，在打开的“创建新任务”对话框中输入“explorer”，单击“确定”按钮后，稍等一下就可以见到桌面图标了。3、问题还没解决，按Windows键+R(或者点开始-->..._上传文件时候怎么找不到桌面图标

LINUX 虚拟网卡tun例子——修改_怎么设置tun的接收缓冲-程序员宅基地

文章浏览阅读1.5k次。参考：http://blog.csdn.net/zahuopuboss/article/details/9259283 #include #include #include #include #include #include #include #include #include #include #include #include _怎么设置tun的接收缓冲

UITextView 评论输入框高度自适应-程序员宅基地

文章浏览阅读741次。创建一个inputView继承于UIView- (instancetype)initWithFrame:(CGRect)frame{ self = [superinitWithFrame:frame]; if (self) { self.backgroundColor = [UIColorcolorWithRed:0.13gre

随便推点

字符串基础面试题_java字符串相关面试题-程序员宅基地

文章浏览阅读594次。字符串面试题（2022）_java字符串相关面试题

VSCODE 实现远程GUI，显示plt.plot，设置x11端口转发_vscode远程ssh连接服务器 python 显示plt-程序员宅基地

文章浏览阅读1.4w次，点赞12次，收藏21次。VSCODE 实现远程GUI，显示plt.plot，设置x11端口转发问题服务器 linux ubuntu16.04本地 windows 10很多小伙伴发现VSCode不能显示figure，只有用自带的jupyter才能勉强个截图、或者转战远程桌面，这对数据分析极为不方便。在命令行键入xeyes（一个显示图像的命令）会failed，而桌面下会出现：但是Xshell能实现X11转发图像，有交互功能，但只能用Xshell输入命令plot，实在不方便。其实VScode有X11转发插件！！方法_vscode远程ssh连接服务器 python 显示plt

Java SE | 网络编程 TCP、UDP协议 Socket套接字的使用_javase套接字socket-程序员宅基地

文章浏览阅读529次。网络编程_javase套接字socket

element-ui switch开关打开和关闭时的文字设置样式-程序员宅基地

文章浏览阅读3.3k次，点赞2次，收藏2次。element switch开关文字显示element中switch开关把on-text 和 off-text 属性改为 active-text 和 inactive-text 属性.怎么把文字描述显示在开关上?下面就是实现方法: 1 <el-table-column label="状态"> 2 <template slot-scope="scope">..._el-switch 不同状态显示不同字

HttpRequestUtil方法get、post、JsonToPost_httprequestutil.httpget-程序员宅基地

文章浏览阅读785次。java后台发起请求使用的工具类package com.cennavi.utils;import org.apache.http.Header;import org.apache.http.HttpResponse;import org.apache.http.HttpStatus;import org.apache.http.client.HttpClient;import org.apache.http.client.methods.HttpPost;import org.apach_httprequestutil.httpget

App-V轻量级应用程序虚拟化之三客户端测试-程序员宅基地

文章浏览阅读137次。在前两节我们部署了App-V Server并且序列化了相应的软件，现在可谓是万事俱备，只欠东风。在这篇博客里面主要介绍一下如何部署客户端并实现应用程序的虚拟化。在这里先简要的说一下应用虚拟化的工作原理吧！App-V Streaming 就是利用templateServer序列化出一个软件运行的虚拟环境，然后上传到app-v Server上，最后客户..._app-v 客户端